练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．某公司新招聘进8名员工，平均分给下属的甲、乙两个部门，其中两名英语翻译人员不能分给同一个部门，另三名电脑编程人员也不能分给同一个部门，则不同的分配方案种数是（　　）
    A．18B．24C．36D．72

    分析 分类讨论：①甲部门要2个2电脑编程人员和一个翻译人员；②甲部门要1个电脑编程人员和1个翻译人员．分别求得这2个方案的方法数，再利用分类计数原理，可得结论．

    解答 解：由题意可得，有2种分配方案：①甲部门要2个电脑编程人员，则有3种情况；翻译人员的分配有2种可能；再从剩下的3个人中选一人，有3种方法．
    根据分步计数原理，共有3×2×3=18种分配方案．
    ②甲部门要1个电脑编程人员，则方法有3种；翻译人员的分配方法有2种；再从剩下的3个人种选2个人，
    方法有3种，共3×2×3=18种分配方案．
    由分类计数原理，可得不同的分配方案共有18+18=36种，
    故选：C．

    点评 本题考查计数原理的运用，根据题意分步或分类计算每一个事件的方法数，然后用乘法原理和加法原理计算，是解题的常用方法，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．已知sin（α+$\frac{π}{3}$）=$\frac{1}{3}$，且α为三角形一内角，则cos（α+$\frac{π}{6}$）的值等于$\frac{-2\sqrt{6}+1}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．计算tan20°-tan80°+$\sqrt{3}$tan20°•tan80°的值是-$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知锐角△ABC中内角A、B、C所对边的边长分别为a、b、c，满足a2+b2=6abcosC，且${sin^2}C=2\sqrt{3}sinAsinB$．
    （Ⅰ）求角C的值；
    （Ⅱ）设函数$f（x）=sin（ωx+\frac{π}{6}）+cosωx_{\;}^{\;}（ω＞0）$，图象上相邻两最高点间的距离为π，求f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．定义集合A-B={x|x∈A且x∉B}，若集合M={1，2，3，4，5}，集合N={x|x=2k-1，k∈Z}，则集合M-N的子集个数为（　　）
    A．2B．3C．4D．无数个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．对于数列{an}，a1=a$+\frac{1}{a}$（a＞0．，且a≠1），an+1=a1-$\frac{1}{{a}_{n}}$．
    （1）求a2，a3，a4，并猜想这个数列的通项公式；
    （2）用数学归纳法证明你的猜想．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知f（x）在R上是减函数，若a=f（log${\;}_{\frac{1}{2}}$8），b=f[（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$]，c=f（2${\;}^{\frac{1}{2}}$）．则（　　）
    A．a＜b＜cB．c＜a＜bC．c＜b＜aD．a＜c＜b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

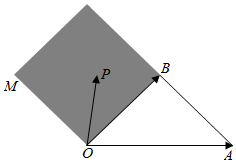    18．如图，OM∥AB，点P在由射线OM，线段OB及AB的延长线围成的阴影区域内（不含边界），且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则实数对（x，y）可以是（　　）
    A．（$\frac{1}{4}$，$\frac{3}{4}$）B．（-$\frac{2}{3}$，$\frac{2}{3}$）C．（-$\frac{1}{4}$，$\frac{3}{4}$）D．（-$\frac{1}{5}$，$\frac{7}{5}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设x＞5，P=$\sqrt{x-4}$-$\sqrt{x-5}$，Q=$\sqrt{x-2}$-$\sqrt{x-3}$，则P与Q的大小关系是P＜Q．

    查看答案和解析>>

    同步练习册答案