Question

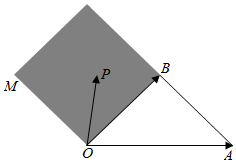
18．如图，OM∥AB，点P在由射线OM，线段OB及AB的延长线围成的阴影区域内（不含边界），且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则实数对（x，y）可以是（　　）

• A． （$\frac{1}{4}$，$\frac{3}{4}$）
• B． （-$\frac{2}{3}$，$\frac{2}{3}$）
• C． （-$\frac{1}{4}$，$\frac{3}{4}$）
• D． （-$\frac{1}{5}$，$\frac{7}{5}$）

Answer 1

分析 利用平面向量的基本定理和平行四边形法则，可以将四个答案一一代入，判断点的位置，排除错误答案，即可得到结论．

解答 解：根据平面向量基本定理和平行四边形法则，
A（$\frac{1}{4}$，$\frac{3}{4}$），$\overrightarrow{OP}$=$\frac{1}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$，此时P在$\overrightarrow{OB}$的下方，
B（-$\frac{2}{3}$，$\frac{2}{3}$），$\overrightarrow{OP}$=-$\frac{2}{3}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$，此时P在OM的上，
D（-$\frac{1}{5}$，$\frac{7}{5}$），$\overrightarrow{OP}$=-$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{7}{5}$$\overrightarrow{OB}$，此时P在直线AB的上方，
因此ABD均不正确，
故选：C．

点评 代入验证法是我们解决选择题最常用的方法之一，其作法是，逐一将答案代入已知条件，逐一验证是否符合题目的要求，如果不符合条件要求，则答案一定是错误的，可直接排除，最后得到正确的答案．