
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
分析 根据F1F2为圆的直径,推断出∠F1PF2为直角,进而可推断出sin∠PF1F2=$\frac{|P{F}_{2}|}{|{F}_{1}{F}_{2}|}$=$\frac{3}{5}$,设P在右支上,|PF2|=t,
由双曲线的定义可得|PF1|=2a+t,利用勾股定理,解方程可得双曲线的离心率.
解答 解:∵F1F2为圆的直径,
∴△PF1F2为直角三角形,
∴sin∠PF1F2=$\frac{|P{F}_{2}|}{|{F}_{1}{F}_{2}|}$=$\frac{3}{5}$,
设P在右支上,|PF2|=t,
由双曲线的定义可得|PF1|=2a+t,
可得t=$\frac{6}{5}$c,
由勾股定理可得4c2=t2+(2a+t)2,
即4c2=($\frac{6}{5}$c)2+(2a+$\frac{6}{5}$c)2,
化简为7c2-30ac-25a2=0,
由e=$\frac{c}{a}$,可得7e2-30e-25=0,
解得e=5(负的舍去),
故选:D.
点评 本题考查双曲线的简单性质的应用,考查离心率的求法,注意运用直角三角形的正弦函数的定义,注意双曲线定义的灵活运用.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
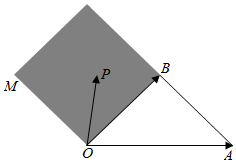 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )| A. | ($\frac{1}{4}$,$\frac{3}{4}$) | B. | (-$\frac{2}{3}$,$\frac{2}{3}$) | C. | (-$\frac{1}{4}$,$\frac{3}{4}$) | D. | (-$\frac{1}{5}$,$\frac{7}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{2}+1$) | B. | ($\sqrt{2}+1,+∞$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,$\sqrt{2}+1$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5}{6}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
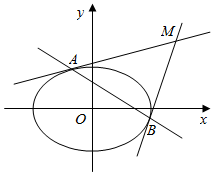 教材器有介绍:圆x2+y2=r2上的点(x0,y0)处的切线方程为x0x+y0y=r2,我们将其结论推广:椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点(x0,y0)处的切线方程为$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}$=1,在解本题时可以直接应用.已知,直线x-y+$\sqrt{3}$=0与椭圆E$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1(a>1)有且只有一个公共点
教材器有介绍:圆x2+y2=r2上的点(x0,y0)处的切线方程为x0x+y0y=r2,我们将其结论推广:椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点(x0,y0)处的切线方程为$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}$=1,在解本题时可以直接应用.已知,直线x-y+$\sqrt{3}$=0与椭圆E$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1(a>1)有且只有一个公共点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | p∨¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com