
| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | p∨¬q |
分析 由函数的翻折和平移,得到命题p假,则¬p真;由函数的奇偶性,对轴称和平移得到命题q假,则命题¬q真,由此能求出结果.
解答 解:函数y=2-ax+1的图象可看作把y=ax的图象先沿轴反折,再左移1各单位,最后向上平移2各单位得到,
而y=ax的图象恒过(0,1),所以函数y=2-ax+1恒过(-1,1)点,所以命题p假,则¬p真.
函数f(x-1)为偶函数,则其对称轴为x=0,而函数f(x)的图象是把y=f(x-1)向左平移了1各单位,
所以f(x)的图象关于直线x=-1对称,所以命题q假,则命题¬q真.
综上可知,命题p∧¬q为真命题.
故选:D.
点评 本题考查命题的真假判断,是中档题,解题时要认真审题,注意得复合命题的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | c>a>b | C. | a>b>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-18,13] | B. | [0,14] | C. | [13,14] | D. | [-18,14] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
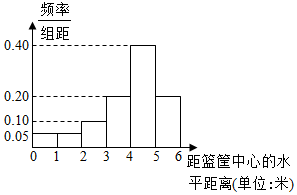 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com