
分析 根据距离公式判断①④,根据三角函数的性质判断②③.
解答 解:①当A,B是x轴上两点时,y1=y2=0,d(A,B)=|x1-x2|显然成立,∴①对;
②由x∈[0,1]得,d(A,B)=|1-cos2θ|+|2-sin2θ|=1-cos2θ+2-sin2θ=2为定值,∴②对;
③由条件得$d(A,B)=|{2-cosθ}|+|{1-sinθ}|=3-\sqrt{2}sin(θ+\frac{π}{4})$,
∴$d(A,B)∈[{3-\sqrt{2},3+\sqrt{2}}]$,∴③不对;
④由条件知${|{AB}|^2}=({x_1}-{x_2}{)^2}+{({y_1}-{y_2})^2}≥\frac{1}{2}{(|{{x_1}-{x_2}}|+|{{y_1}-{y_2}}|)^2}$,
∴$|{AB}|=≥\frac{{\sqrt{2}}}{2}(|{{x_1}-{x_2}}|+|{{y_1}-{y_2}}|)=\frac{{\sqrt{2}}}{2}d(A,B)$,∴④对;
故答案为:①②④.
点评 本题考查了两点间距离公式的应用,考查三角函数问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
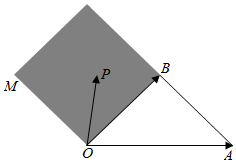 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )| A. | ($\frac{1}{4}$,$\frac{3}{4}$) | B. | (-$\frac{2}{3}$,$\frac{2}{3}$) | C. | (-$\frac{1}{4}$,$\frac{3}{4}$) | D. | (-$\frac{1}{5}$,$\frac{7}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com