Question

【题目】如图，直三棱柱ABC﹣A1B1C1中，AA1=AB=AC=2，D，E，F分别是B1A1 ， CC1 ， BC的中点，AE⊥A1B1 ， D为棱A1B1上的点．

（1）证明：DF⊥AE；
（2）求平面DEF与平面ABC所成锐二面角的余弦值．

Answer 1

【答案】
（1）证明：∵AE⊥A1B1，A1B1∥AB，

∴AB⊥AE，又∵AB⊥AA1，AE∩AA1=A，

∴AB⊥面A1ACC1，又∵AC面A1ACC1，

∴AB⊥AC，

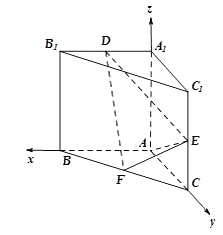
以A为原点，分别以AB，AC，AA1所在直线为x，y，z轴，

建立空间直角坐标系，

则A（0，0，0），E（0，2，1），F（1，1，0），A1（0，0，2），B1（2，0，2），

设D（x，y，z）， =λ ，且λ∈[0，1]，

即（x，y，z﹣2）=λ（2，0，0），∴D（2λ，0，2），

∴ =（1﹣2λ，1，﹣2）， =（0，2，1），

∵ =0+2﹣2=0，

∴DF⊥AE

（2）解： D（1，0，2），E（0，2，1），F（1，1，1），

=（﹣1，2，﹣1）， =（0，1，﹣1），

设平面DEF的法向量 =（x，y，z），

则 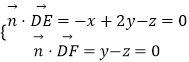，取y=1，得 =（1，1，1），

平面ABC的法向量 =（0，0，1），

cos＜ ＞= = ．

∴平面DEF与平面ABC所成锐二面角的余弦值为 ．

【解析】（1）推导出AB⊥AE，AB⊥AA1 ， 从而AB⊥面A1ACC1 ， 由此能证明AB⊥AC，以A为原点，分别以AB，AC，AA1所在直线为x，y，z轴，建立空间直角坐标系，利用向量法能证明DF⊥AE．（2）求出平面DEF的法向量和平面ABC的法向量，利用向量法能求出平面DEF与平面ABC所成锐二面角的余弦值．
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识，掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．