
分析 (Ⅰ)利用点P到两个顶点M(-1,0),N(1,0)距离的比为$\sqrt{2}$,建立等式,化简,即可求得动点P的轨迹C的方程;
(Ⅱ)设出直线方程,代入轨迹C的方程,利用韦达定理,证明kBN-kQN=0,即可得出结论.
解答 (Ⅰ)解:设P(x,y),则
∵点P到两个顶点M(-1,0),N(1,0)距离的比为$\sqrt{2}$,
∴$\sqrt{(x+1)^{2}+{y}^{2}}$=$\sqrt{2}•\sqrt{(x-1)^{2}+{y}^{2}}$,
整理得x2+y2-6x+1=0,
∴动点P的轨迹C的方程是x2+y2-6x+1=0;
(Ⅱ)证明:由题意,直线l存在斜率,设为k(k≠0),直线l的方程为y=k(x+1)
代入x2+y2-6x+1=0,
化简得(1+k2)x2+(2k2-6)x+k2+1=0,
△>0,可得-1<k<1.
设A(x1,y1),B(x2,y2),则Q(x1,-y1),且x1x2=1,
∴kBN-kQN=$\frac{{y}_{2}}{{x}_{2}-1}$-$\frac{-{y}_{1}}{{x}_{1}-1}$=$\frac{2k({x}_{1}{x}_{2}-1)}{({x}_{1}-1)({x}_{2}-1)}$=0,
∴B,N,Q在同一条直线上.
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查韦达定理的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
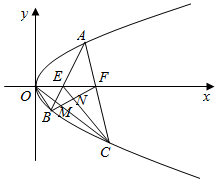 如图,点A(x1,y1),B(x2,y2),C(x3,y3)(y1>0,y2<0,y3<0)是抛物线y2=2px(p>0)上不同三点,AB,AC分别与x轴交于点E、F,BF与OC,EC分别交于M,N,则( )
如图,点A(x1,y1),B(x2,y2),C(x3,y3)(y1>0,y2<0,y3<0)是抛物线y2=2px(p>0)上不同三点,AB,AC分别与x轴交于点E、F,BF与OC,EC分别交于M,N,则( )| A. | S△OBM=S△ENF+S△MNC | B. | S△OBM=S△ENF-S△MNC | ||
| C. | S△OBM+S△ENF=S△MNC | D. | S△OBM+S△ENF=2S△MNC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{4}$,$\frac{π}{2}$] | C. | [$\frac{π}{12}$,$\frac{π}{2}$] | D. | [$\frac{π}{12}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1} | C. | [0,1] | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
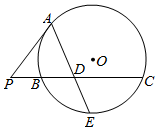 如图,切线PA切圆O于点A,割线PBC与圆O交于点B,C,且PC=2PA,D为线段PC的中点,AD的延长线交圆O于点E.若PB=$\frac{3}{4}$,则AD•DE的值为$\frac{9}{8}$.
如图,切线PA切圆O于点A,割线PBC与圆O交于点B,C,且PC=2PA,D为线段PC的中点,AD的延长线交圆O于点E.若PB=$\frac{3}{4}$,则AD•DE的值为$\frac{9}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{45}{2}$ | B. | 45 | C. | $\frac{135}{2}$ | D. | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com