
分析 转化成指数式t+1<(1+$\frac{t}{n}$)n.再对指数式利用二项定理展开,结合放缩法证得即可
解答 证明:要证证:$\root{n}{a}$-1<$\frac{a-1}{n}$,
即证a<($\frac{a-1}{n}$+1)n.
令a-1=t>0,则a=t+1.
也就是证t+1<(1+$\frac{t}{n}$)n.
∵(1+$\frac{t}{n}$)n=1+Cn1$\frac{t}{n}$+…+Cnn($\frac{t}{n}$)n>1+t,
即证:$\root{n}{a}$-1<$\frac{a-1}{n}$成立.
点评 本题考查不等式的证明,本题还考查了二项式定理的展开式,一般地,涉及不等关系的指数式可应用二项式定理展开后进行放缩,属于中档题.


科目:高中数学 来源: 题型:选择题
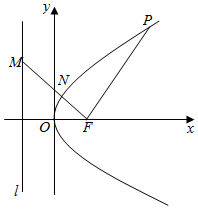 如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )
如图,P为抛物线C:y2=8x上一点,F为抛物线的焦点,M为抛物线准线l上一点,且MF⊥PF,线段MF与抛物线交于点N,若|PF|=8,则$\frac{|MN|}{|NF|}$=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{2}}{6}$ | B. | 3$\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com