
分析 (1)把已知数列递推式变形,可得${a}_{n+1}-{a}_{n}=\frac{{a}_{n}}{1-\frac{1}{{a}_{n+1}{a}_{n}}}$,结合0<an<1,得到an+1-an=$\frac{{a}_{n}}{1-\frac{1}{{a}_{n+1}{a}_{n}}}$<0,即an+1<an;
(2)由已知数列递推式得${a}_{n}={a}_{n+1}-{a}_{n}+\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$,利用累加法得到Sn=${a}_{n+1}-{a}_{1}+\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{1}}$=an+1+$\frac{1}{{a}_{n+1}}$$-\frac{5}{2}$.把已知递推式两边平方可得${{a}_{n+1}}^{2}+2+\frac{1}{{{a}_{n+1}}^{2}}=4{{a}_{n}}^{2}+4+\frac{1}{{{a}_{n}}^{2}}$,利用放缩法得到$2<\frac{1}{{{a}_{n+1}}^{2}}-\frac{1}{{{a}_{n}}^{2}}<3$,即2n$<\frac{1}{{{a}_{n+1}}^{2}}-\frac{1}{{{a}_{1}}^{2}}<3n$,进一步得到$\sqrt{2n+4}<\frac{1}{{a}_{n+1}}<\sqrt{3n+4}$,然后利用不等式的可加性证得$\sqrt{2n+4}$-$\frac{5}{2}$<Sn<$\sqrt{3n+4}$-2.
解答 证明:(1)由an+1+$\frac{1}{{a}_{n+1}}$=2an+$\frac{1}{{a}_{n}}$,
得${a}_{n+1}-{a}_{n}+\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}={a}_{n}$,即$({a}_{n+1}-{a}_{n})-\frac{{a}_{n+1}-{a}_{n}}{{a}_{n+1}{a}_{n}}={a}_{n}$,
∴${(a}_{n+1}-{a}_{n})(1-\frac{1}{{a}_{n+1}{a}_{n}})={a}_{n}$,则${a}_{n+1}-{a}_{n}=\frac{{a}_{n}}{1-\frac{1}{{a}_{n+1}{a}_{n}}}$,
又0<an<1,
∴${a}_{n+1}-{a}_{n}=\frac{{a}_{n}}{1-\frac{1}{{a}_{n+1}{a}_{n}}}<0$,即an+1<an;
(2)由an+1+$\frac{1}{{a}_{n+1}}$=2an+$\frac{1}{{a}_{n}}$,得${a}_{n}={a}_{n+1}-{a}_{n}+\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$.
∴Sn=a1+a2+…+an=$({a}_{2}-{a}_{1})+(\frac{1}{{a}_{2}}-\frac{1}{{a}_{1}})+({a}_{3}-{a}_{2})+(\frac{1}{{a}_{3}}-\frac{1}{{a}_{2}})$+…+$({a}_{n+1}-{a}_{n})+(\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}})$
=${a}_{n+1}-{a}_{1}+\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{1}}={a}_{n+1}+\frac{1}{{a}_{n+1}}-\frac{5}{2}$.
又∵an+1+$\frac{1}{{a}_{n+1}}$=2an+$\frac{1}{{a}_{n}}$,
∴${{a}_{n+1}}^{2}+2+\frac{1}{{{a}_{n+1}}^{2}}=4{{a}_{n}}^{2}+4+\frac{1}{{{a}_{n}}^{2}}$,
∴$\frac{1}{{{a}_{n+1}}^{2}}=\frac{1}{{{a}_{n}}^{2}}+2+4{{a}_{n}}^{2}-{{a}_{n+1}}^{2}$.
由0<an+1<an,可知$\frac{1}{{{a}_{n}}^{2}}+2<\frac{1}{{{a}_{n+1}}^{2}}<\frac{1}{{{a}_{n}}^{2}}+2+4{{a}_{1}}^{2}=\frac{1}{{{a}_{n}}^{2}}+3$,
即$2<\frac{1}{{{a}_{n+1}}^{2}}-\frac{1}{{{a}_{n}}^{2}}<3$,
∴2n$<\frac{1}{{{a}_{n+1}}^{2}}-\frac{1}{{{a}_{1}}^{2}}<3n$,
∴$2n+4<\frac{1}{{{a}_{n+1}}^{2}}<3n+4$,$\sqrt{2n+4}<\frac{1}{{a}_{n+1}}<\sqrt{3n+4}$,
∵$0<{a}_{n+1}<\frac{1}{2}$.
∴$\sqrt{2n+4}-\frac{5}{2}<{a}_{n+1}+\frac{1}{{a}_{n+1}}-\frac{5}{2}<\sqrt{3n+4}-2$.
∴$\sqrt{2n+4}$-$\frac{5}{2}$<Sn<$\sqrt{3n+4}$-2.
点评 本题考查数列递推式,考查了裂项相消法求数列的和,训练了利用放缩法证明数列不等式,考查逻辑思维能力和推理运算能力,难度较大.


 同步轻松练习系列答案
同步轻松练习系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{2}}{6}$ | B. | 3$\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
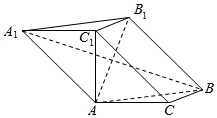 在三棱柱ABC-A1B1C1中,AC⊥BC,AC1⊥平面ABC,BC=CA=AC1.
在三棱柱ABC-A1B1C1中,AC⊥BC,AC1⊥平面ABC,BC=CA=AC1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com