
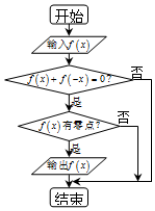
 某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.
某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.分析 根据程序框图得到第一个条件为判断函数是否是奇函数,第二个条件判断函数是否有零点,然后根据函数的性质进行判断即可.
解答 解:第一个条件为判断函数是否是奇函数,第二个条件判断函数是否有零点,
①f(x)=$\frac{sinx}{{x}^{2}}$ 是奇函数,由f(x)=0得sinx=0且x≠0,函数存在零点,满足条件.
②由f(x)=ln($\sqrt{{x}^{2}+1}$+x),得f(-x)+f(x)=ln($\sqrt{{x}^{2}+1}$+x)+ln($\sqrt{{x}^{2}+1}$-x)=ln($\sqrt{{x}^{2}+1}$+x)($\sqrt{{x}^{2}+1}$-x)=ln(1+x2-x2)=ln1=0,
当x=0时,f(x)=0,则满足函数有零点,满足条件.
③f(x)=$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$,满足f(-x)=-f(x),且当x=0时,f(0)=0,满足条件.
④f(x)=$\frac{si{n}^{2}x}{1+co{s}^{2}x}$.得f(-x)=f(x),函数是偶函数,不满足第一个条件.
故答案为:①②③
点评 本题主要考查程序框图的应用,根据函数的性质得到第一个条件为判断函数是否是奇函数,第二个条件判断函数是否有零点是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [4,+∞) | C. | [8,+∞) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100π}{3}$ | B. | 64π | C. | 100π | D. | $\frac{500π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
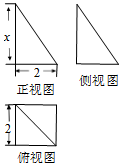
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com