
分析 由条件利用正弦函数的周期性、单调性,y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:(1)对于f(x)=sin(2x+$\frac{π}{6}$)+$\frac{3}{2}$,x∈R,它的周期为 T=$\frac{2π}{2}$=π.
(2)由2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,k∈Z,
所以所求的单调减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
(3)把y=sin2x的图象上所有点向左平移$\frac{π}{12}$个单位,可得y=sin(2x+$\frac{π}{6}$)的图象;
再向上平移$\frac{3}{2}$个单位,即得函数f(x)=sin(2x+$\frac{π}{6}$)+$\frac{3}{2}$的图象.
点评 本题主要考查正弦函数的周期性、单调性,y=Asin(ωx+φ)的图象变换规律,属于基础题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-∞,-2014) | C. | (-∞,-2018) | D. | (-2018,-2014) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则$\overline{AM}•\overline{DC}$的最大值是( )
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则$\overline{AM}•\overline{DC}$的最大值是( )| A. | $8+4\sqrt{5}$ | B. | $8-4\sqrt{5}$ | C. | $4+8\sqrt{5}$ | D. | $8\sqrt{5}-4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{1-{k}^{2}}}{k}$ | B. | -$\frac{\sqrt{1-{k}^{2}}}{k}$ | C. | $\frac{k}{\sqrt{1-{k}^{2}}}$ | D. | -$\frac{k}{\sqrt{1-{k}^{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$) | C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)∥($\overrightarrow{a}$-$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
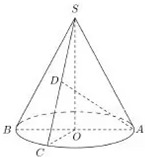 如图,在圆锥SO中,AB为底面圆O的直径,点C为弧$\widehat{AB}$的中点,SO=AB;
如图,在圆锥SO中,AB为底面圆O的直径,点C为弧$\widehat{AB}$的中点,SO=AB;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com