
分析 (1)据切点处的导数值为曲线切线斜率,由二次函数的秋雨求法,求导函数的范围也就是切线斜率范围;
(2)互相垂直的切线斜率互为负倒数,由(1)求斜率范围,据切点处的导数值为曲线切线斜率,解不等式,求切点横坐标范围.
解答 解:(1)函数f(x)=$\frac{1}{3}$x3-2x2+3x的导数为f′(x)=x2-4x+3
=(x-2)2-1≥-1,
即过曲线C上任意一点的切线斜率的取值范围是[-1,+∞);
(2)设其中一条切线的斜率为k,另一条为-$\frac{1}{k}$,
由(1)可知,$\left\{\begin{array}{l}{k≥-1}\\{-\frac{1}{k}≥-1}\end{array}\right.$,
解得-1≤k<0或k≥1,
由-1≤x2-4x+3<0或x2-4x+3≥1,
即有1<x<3或x≥2+$\sqrt{2}$或x≤2-$\sqrt{2}$,
得:x∈(-∞,2-$\sqrt{2}$]∪(1,3)∪[2+$\sqrt{2}$,+∞).
点评 本题考查切点处的导数值为曲线切线斜率,考查两直线垂直的条件:斜率之积为-1,以及化简整理的运算能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
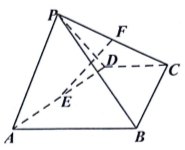 如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.
如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份202x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数 y(十万) | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\stackrel{∧}{y}$=-10x-100 | B. | $\stackrel{∧}{y}$=10x-100 | C. | $\stackrel{∧}{y}$=-10x+200 | D. | $\stackrel{∧}{y}$=10x-200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
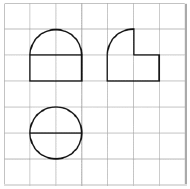
| A. | $\frac{7π}{2}$ | B. | 4π | C. | $\frac{9π}{2}$ | D. | 5π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com