
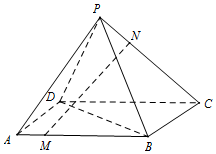
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,且PA=PB=PC=PD,MB=2AM,CN=2PN
如图,在四棱锥P-ABCD中,底面ABCD是正方形,且PA=PB=PC=PD,MB=2AM,CN=2PN分析 (1)作NQ∥CD,交PD于Q,连接AQ,证明:四边形AMNQ为平行四边形,可得MN∥AQ,即可证明MN∥面PAD;
(2)连接AC,与BD交于H,连接PH,证明:BD⊥平面PAC,即可证明BD⊥PC.
解答  证明:(1)作NQ∥CD,交PD于Q,连接AQ,
证明:(1)作NQ∥CD,交PD于Q,连接AQ,
∵CN=2PN,∴NQ=$\frac{1}{3}$CD,
∵AM=$\frac{1}{3}$AB=$\frac{1}{3}CD$,AB∥CD,
∴AM∥NQ,AM=NQ,
∴四边形AMNQ为平行四边形,
∴MN∥AQ,
∵MN?平面PAD,QA?平面PAD,
∴MN∥面PAD
(2)连接AC,与BD交于H,
∵ABCD为正方形,
∴H为AC,BD的中点,AC⊥BD,
连接PH,
∵PB=PD,
∴PH⊥BD,
∵AC⊥BD,AC∩PH=H,
∴BD⊥平面PAC,
∵PC?平面PAC,
∴BD⊥PC.
点评 本题考查线面平行的判定,考查线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
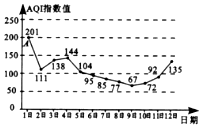 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )| A. | 这12天中有6天空气质量为“优良” | B. | 这12天中空气质量最好的是4月9日 | ||
| C. | 这12天的AQI指数值的中位数是90 | D. | 从4日到9日,空气质量越来越好 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 余江人热情好客,凡逢喜事,一定要摆上酒宴,请亲朋好友、同事高邻来助兴庆贺.欢度佳节,迎亲嫁女,乔迁新居,学业有成,仕途风顺,添丁加口,朋友相聚,都要以酒示意,借酒表达内心的欢喜.而凡有酒宴,一定要划拳,划拳是余江酒文化的特色.余江人划拳注重礼节,形式多样;讲究规矩,蕴含着浓厚的传统文化和淳朴的民俗特色.在礼节上,讲究“尊老尚贤敬远客”一般是东道主自己或委托桌上一位酒量好的划拳高手来“做关”,--就是依次陪桌上会划拳的划一年数十二拳(也有半年数六拳).十二拳之后晚辈还要敬长辈一杯酒.
余江人热情好客,凡逢喜事,一定要摆上酒宴,请亲朋好友、同事高邻来助兴庆贺.欢度佳节,迎亲嫁女,乔迁新居,学业有成,仕途风顺,添丁加口,朋友相聚,都要以酒示意,借酒表达内心的欢喜.而凡有酒宴,一定要划拳,划拳是余江酒文化的特色.余江人划拳注重礼节,形式多样;讲究规矩,蕴含着浓厚的传统文化和淳朴的民俗特色.在礼节上,讲究“尊老尚贤敬远客”一般是东道主自己或委托桌上一位酒量好的划拳高手来“做关”,--就是依次陪桌上会划拳的划一年数十二拳(也有半年数六拳).十二拳之后晚辈还要敬长辈一杯酒.| A. | $\frac{4}{9}$ | B. | $\frac{8}{27}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬q)为真命题 | B. | p∨(¬q)为真命题 | C. | (¬p)∧(¬q)为真命题 | D. | p∨q为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2-1 | B. | 1-1n2 | C. | 1n2 | D. | -1n2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com