
| A. | n2-1 | B. | 1-1n2 | C. | 1n2 | D. | -1n2 |
分析 求出f(x)-g(x)的解析式,令$h(x)=x-\frac{1}{2}ln(2x+1)$,根据函数的单调性求出h(x)的最小值,结合不等式的性质求出对应的a的值即可.
解答 解:f(x)-g(x)=$x-\frac{1}{2}ln(2x+1)+{e^{x-a}}+4{e^{a-x}}$,
令$h(x)=x-\frac{1}{2}ln(2x+1)$,则$h'(x)=1-\frac{1}{2x+1}$,
知h(x)在$(-\frac{1}{2},0)$上是减函数,在(0,+∞)上是增函数,所以h(x)min=h(0)=0,
又${e^{x-a}}+4{e^{a-x}}≥2\sqrt{{e^{x-a}}•4{e^{a-x}}}=4$
所以f(x)-g(x)≥4,
当且仅当$\left\{\begin{array}{l}x=0\\{e^{x-a}}=4{e^{a-x}}\end{array}\right.$即x=0,a=-ln2,
故选:D.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的性质,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
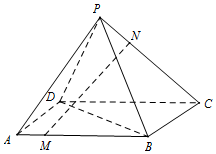 如图,在四棱锥P-ABCD中,底面ABCD是正方形,且PA=PB=PC=PD,MB=2AM,CN=2PN
如图,在四棱锥P-ABCD中,底面ABCD是正方形,且PA=PB=PC=PD,MB=2AM,CN=2PN查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
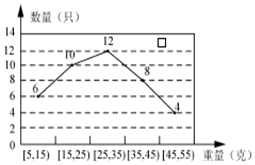 某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,45) | [45,55] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
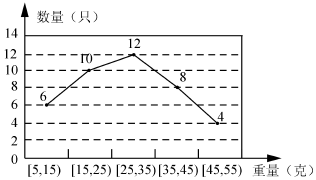
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,35) | [35,55] |
| 单价(元/只) | 1.2 | 1.5 | 1.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com