
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,35) | [35,55] |
| 单价(元/只) | 1.2 | 1.5 | 1.8 |
分析 (1)根据古典概率的定义即可求出,
(2)根据平均数的定义即可求出,
(3)设该经销商收购这批小龙虾每千克至多x元,根据分层抽样即可求出.
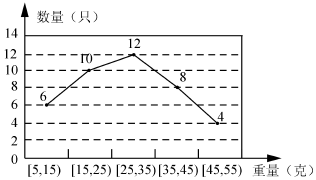
解答 解:(1)由于40只小龙虾中重量不超过35g的小龙虾有6+10+12=28(只),
所以$P(A)=\frac{28}{40}=\frac{7}{10}$;
(2)从统计图中可以估计这批小龙虾的平均重量为$\frac{1}{40}(6×10+10×20+12×30+8×40+4×50)$=$\frac{1140}{40}=28.5$(克),
(3)设该经销商收购这批小龙虾每千克至多x元.根据样本,由(2)知,这40只小龙虾中一等品、二等品、三等品各有16只、12只、12只,约有1140g,
所以1140x≤16×1.2+12×1.5+12×1.8,而$\frac{16×1.2+12×1.5+12×1.8}{1140}≈51.6$,
故可以估计该经销商收购这批小龙虾每千克至多51元.
点评 本题考查了古典概率和平均数和分层抽样的问题,考查了分析问题解决问题的能力,属于基础题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2-1 | B. | 1-1n2 | C. | 1n2 | D. | -1n2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,顶点为A1、A2、B1、B2,且$\overrightarrow{{A_1}{B_1}}•\overrightarrow{{A_1}{B_2}}=3$.
如图,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,顶点为A1、A2、B1、B2,且$\overrightarrow{{A_1}{B_1}}•\overrightarrow{{A_1}{B_2}}=3$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6种 | B. | 12种 | C. | 18种 | D. | 24种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
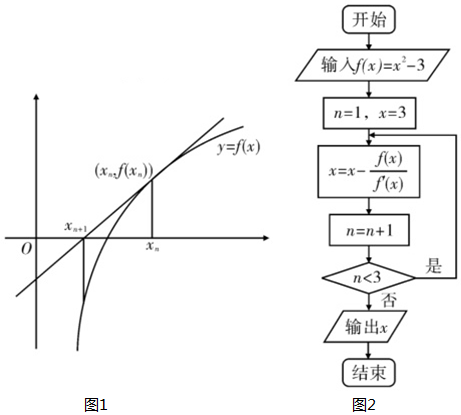
| A. | 2 | B. | 1.75 | C. | 1.732 | D. | 1.73 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com