
分析 数列{an}满足a1=1,且an+1-an=n+1,n∈N*,利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1与等差数列的求和公式可得an,再利用裂项求和方法即可得出.
解答 解:∵数列{an}满足a1=1,且an+1-an=n+1,n∈N*,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n+(n-1)+…+2+1
=$\frac{n(n+1)}{2}$.
∴$\frac{1}{{a}_{n}}$=2$(\frac{1}{n}-\frac{1}{n+1})$.
∴数列$\left\{{\frac{1}{a_n}}\right\}$的前n项和Sn=2$[(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=2$(1-\frac{1}{n+1})$=$\frac{2n}{n+1}$.
故答案为:$\frac{2n}{n+1}$.
点评 本题考查了累加求和方法、“裂项求和”方法、等差数列的求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
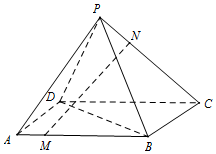 如图,在四棱锥P-ABCD中,底面ABCD是正方形,且PA=PB=PC=PD,MB=2AM,CN=2PN
如图,在四棱锥P-ABCD中,底面ABCD是正方形,且PA=PB=PC=PD,MB=2AM,CN=2PN查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
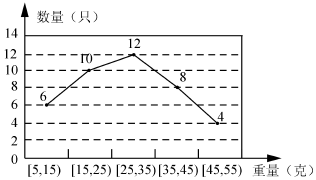
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,35) | [35,55] |
| 单价(元/只) | 1.2 | 1.5 | 1.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com