
分析 (Ⅰ)由题意可知a2-3=1,即可求得a的值,求得椭圆方程;
(Ⅱ)(ⅰ)根据向量数量积的坐标运算,即可求得mn=3,由|AF1|=|BF1|,求得m2-n2=8,即可求得m和n的值,求得三角形的面积;
(ⅱ)直线$AB:y=\frac{n-m}{4}(x+2)+m$,利用点到直线的距离公式,由点F1,F2在直线AB的同一侧,利用基本不等式的性质,即可求得点F1,F2到直线AB距离之和的最小值.
解答 解:(Ⅰ)由题意可得,c=1,则a2-b2=c2,即a2-3=1,
则a2=4,
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)(ⅰ)由题意可设A(-2,m),B(2,n),
由AF1⊥BF1,则$\overrightarrow{A{F_1}}•\overrightarrow{B{F_1}}=0$,即(1,-m)(-3,-n)=0,则mn=3,①
由AF1⊥BF1,则当△ABF1为等腰三角形时,只能是|AF1|=|BF1|,即$\sqrt{{m^2}+1}=\sqrt{9+{n^2}}$,
化简得m2-n2=8,②
由①②可得$\left\{{\begin{array}{l}{m=3}\\{n=1}\end{array}}\right.$或$\left\{{\begin{array}{l}{m=-3}\\{n=-1}\end{array}}\right.$,
∴${S_{△AB{F_1}}}=\frac{1}{2}|A{F_1}||B{F_1}|=\frac{1}{2}{\sqrt{10}^2}=5$.
(ⅱ)直线$AB:y=\frac{n-m}{4}(x+2)+m$,
化简得(n-m)x-4y+2(m+n)=0,
由点到直线的距离公式可得点F1,F2到直线AB距离之和为
${d_1}+{d_2}=\frac{|2(m+n)-(n-m)|}{{\sqrt{{{(n-m)}^2}+16}}}+\frac{|2(m+n)+(n-m)|}{{\sqrt{{{(n-m)}^2}+16}}}$
∵点F1,F2在直线AB的同一侧,
∴${d_1}+{d_2}=\frac{4|m+n|}{{\sqrt{{{(n-m)}^2}+16}}}=4\sqrt{\frac{{{m^2}+{n^2}+2mn}}{{{m^2}+{n^2}-2mn+16}}}$
由mn=3,
则m2+n2≥2mn=6,${d_1}+{d_2}=4\sqrt{\frac{{{m^2}+{n^2}+6}}{{{m^2}+{n^2}+10}}}=4\sqrt{1-\frac{4}{{{m^2}+{n^2}+10}}}$
∴${d_1}+{d_2}=4\sqrt{1-\frac{4}{{{m^2}+{n^2}+10}}}≥2\sqrt{3}$
当$m=n=\sqrt{3}$或$m=n=-\sqrt{3}$时,点F1,F2到直线AB距离之和取得最小值$2\sqrt{3}$.
∴点F1,F2到直线AB距离之和取得最小值$2\sqrt{3}$.
点评 本题考查椭圆的标准方程及简单几何性质,向量数量积的坐标运算,点到直线的距离公式,基本不等式的性质,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6种 | B. | 12种 | C. | 18种 | D. | 24种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 21 | C. | 25 | D. | 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
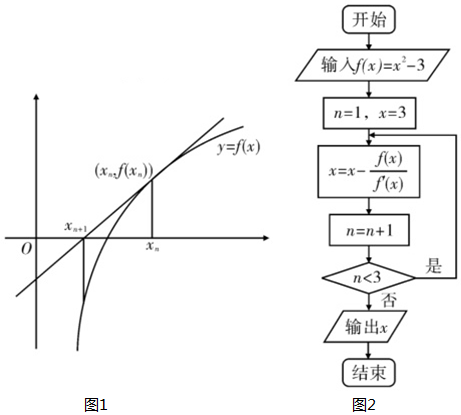
| A. | 2 | B. | 1.75 | C. | 1.732 | D. | 1.73 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com