
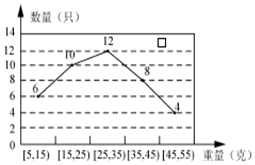
 某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,45) | [45,55] |
分析 (1)由于40只小龙虾中重量不超过35g的小龙虾有6+10+12(只),利用古典概率计算公式即可得出.
(2)求出其平均数,可得从统计图中可以估计每只小龙虾的重量.
(3)由题意知抽取一等品、二等品、三等品分别为4只、5只、1只,X=0,1,2,3.利用超几何分布列的概率
的计算公式即可得出.
解答 解:(1)由于40只小龙虾中重量不超过35g的小龙虾有6+10+12=28(只)
所以$P(A)=\frac{28}{40}=\frac{7}{10}$.
(2)从统计图中可以估计每只小龙虾的重量$\frac{1}{40}(6×10+10×20+12×30+8×40+4×50)$
=$\frac{1140}{40}=28.5$(克)
所以购进100千克,小龙虾的数量约有100000÷28.5≈3509(只)
(3)由题意知抽取一等品、二等品、三等品分别为4只、5只、1只,X=0,1,2,3
则可得$P(X=0)=\frac{C_5^0C_5^3}{{C_{10}^3}}=\frac{10}{120}=\frac{1}{12}$,$P(X=1)=\frac{C_5^1C_5^2}{{C_{10}^3}}=\frac{50}{120}=\frac{5}{12}$,
$P(X=2)=\frac{C_5^2C_5^1}{{C_{10}^3}}=\frac{50}{120}=\frac{5}{12}$,$P(X=3)=\frac{C_5^3C_5^0}{{C_{10}^3}}=\frac{10}{120}=\frac{1}{12}$
所以$E(X)=0×\frac{1}{12}+1×\frac{5}{12}+2×\frac{5}{12}+3×\frac{1}{12}=\frac{3}{2}$.
点评 本题考查了超几何分布列及其数学期望、古典概率计算公式、平均数的计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬q)为真命题 | B. | p∨(¬q)为真命题 | C. | (¬p)∧(¬q)为真命题 | D. | p∨q为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2-1 | B. | 1-1n2 | C. | 1n2 | D. | -1n2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com