
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据函数的单调性和奇偶性,得到关于x的不等式,解出即可.
解答 解:由f(x)是偶函数且当x≤0时,f(x)为增函数,
则x>0时,f(x)是减函数,
故由“f[log2(2x-2)]>f(log${\;}_{\frac{1}{2}}$$\frac{2}{3}$)”,
得:-log2$\frac{3}{2}$<log2(2x-2)<log2$\frac{3}{2}$,
故$\frac{2}{3}$<2x-2<$\frac{3}{2}$,
解得:$\frac{4}{3}$<x<$\frac{7}{4}$,
故“$\frac{6}{5}$<x<2”是“$\frac{4}{3}$<x<$\frac{7}{4}$“的既不充分也不必要条件,
故选:B.
点评 本题考查了函数的单调性、奇偶性问题,考查对数函数的性质,是一道中档题.


科目:高中数学 来源: 题型:解答题
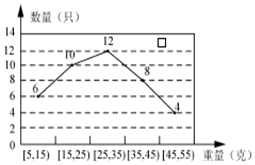 某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,45) | [45,55] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 4031 | D. | 4033 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com