
分析 (1)由条件利用等差数列、等比数列的定义和性质求出首项和公差、公比,从而求得数列{an}及{bn}的通项公式.
(2)哟条件利用前n项和公式求得等比数列{an}的前10项和S10、等差数列{bn}前50项和 T50 的值,再求得A与B的公共元素的和,从而求得集合C中所有元素之和.
解答 解:(1)因为S3=7,∴a1+a2 +a3=7.
因为a1+3,3a2,a3+4成等差数列,所以,a1+3,+a3+4=6a2 ,求得a2 =a1•q=2 ①.
又由a1+a2 +a3=7得a1 +a1•q2=5 ②,
由①②可得 2q2-5q+2=0,解得q=2,或q=$\frac{1}{2}$(舍去),∴a1=1,an =2n-1.
另由于{bn}满足关系式bn(3n-5)=bn-1(3n-2),即 $\frac{{b}_{n}}{{b}_{n-1}}$=$\frac{3n-2}{3n-5}$.
所以由累乘法得 $\frac{{b}_{n}}{{b}_{1}}$=3n-2,而b1=1,所以 bn=3n-2 (n≥2),当n=1时也满足,
故bn=3n-2.
(2)等比数列{an}的前n项和为Sn,则 S10=$\frac{1{-2}^{10}}{1-2}$=1023.
等差数列{bn}前n项和为Tn,则 T50=$\frac{50×(1+148)}{2}$=3725,
因为A与B的公共元素有1,4,16,64,其和为85,
所以集合C中所有元素之和为1023+3725-85=4663.
点评 本题主要考查等差数列及等比数列的定义、性质、通项公式,前n项和公式的应用,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
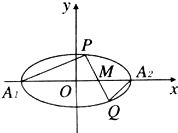 若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.
若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 科目 | 男 | 女 |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com