
���� �����衰�츮����ΪA��B������è����ΪC��D���оٿɵò��Żصij�ȡ�Ļ����¼���6���������������5�������¼����ɸ��ʹ�ʽ�ɵã�
�����оٿɵ��зŻصij�ȡ�Ļ����¼���16�����¼��Ķ����¼���4�������¼����ɶ����¼��ĸ��ʹ�ʽ�ɵã�
��� �⣺�����衰�츮����ΪA��B������è����ΪC��D��
���Żصij�ȡ�Ļ����¼�����A��B������A��C������A��D������B��C������B��D������C��D����6����
�ǡ������߲��Żس齱��Ϊ�¼�A1�����¼�A1������A��C������A��D������B��C������B��D������C��D����5�������¼���
��P��A1��=$\frac{5}{6}$��
�����зŻصij�ȡ�Ļ����¼�����A��A����A��B������A��C������A��D������B��A����B��B������B��C������B��D����
��C��A����C��B������C��C������C��D������D��A����D��B������D��C������D��D����16����
�ǡ��������зŻس齱��Ϊ�¼�B1�����¼�B1�Ķ����¼�����A��A������B��B������A��B������B��A����4�������¼���
��P��B1��=1-$\frac{4}{16}$=$\frac{3}{4}$��
���� ���⿼���оٷ���������¼����¼������ĸ��ʣ��漰�����¼��ĸ��ʹ�ʽ���������⣮


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
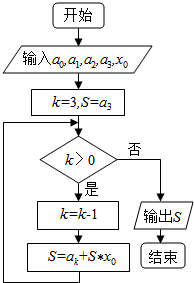
| A�� | a1+x0��a3+x0��a0+a2x0������ֵ | B�� | a3+x0��a2+x0��a1+a0x0������ֵ | ||
| C�� | a0+x0��a1+x0��a2+a3x0������ֵ | D�� | a2+x0��a0+x0��a3+a1x0������ֵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֵ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
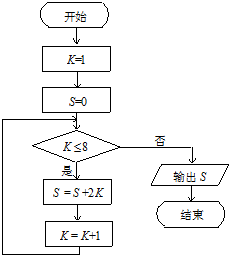
| A�� | 42 | B�� | 56 | C�� | 72 | D�� | 90 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com