
分析 由题意,就是求M到DD1与CC1距离和的最小值,由于A1F在平面ABCD上的射影为AF,故问题转化为正方形ABCD中,AF上的点到D,C距离和的最小值.
解答 解:由题意,就是求M到DD1与CC1距离和的最小值,由于A1F在平面ABCD上的射影为AF,故问题转化为正方形ABCD中,AF上的点到D,C距离和的最小值,设出D关于AF的对称点D',则DD′=$\frac{4\sqrt{5}}{5}$,cos∠CDD′=$\frac{1}{\sqrt{5}}$
∴CD′=$\sqrt{1+\frac{16}{5}-2×1×\frac{4\sqrt{5}}{5}×\frac{1}{\sqrt{5}}}$=$\frac{\sqrt{65}}{5}$,
∴△MDD1与△MCC1的面积和的最小值是$\frac{1}{2}$×$\frac{\sqrt{65}}{5}$=$\frac{\sqrt{65}}{10}$,
故答案为:$\frac{\sqrt{65}}{10}$.
点评 本题考查棱柱的结构特征,考查余弦定理的运用,考查学生分析解决问题的能力,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,两人分别从A村出发,其中一人沿北偏东60°方向行走了1km到了B村,另一人沿北偏西30°方向行走了$\sqrt{3}$km到了C村,问B、C两村相距多远?B村在C村的什么方向上?
如图所示,两人分别从A村出发,其中一人沿北偏东60°方向行走了1km到了B村,另一人沿北偏西30°方向行走了$\sqrt{3}$km到了C村,问B、C两村相距多远?B村在C村的什么方向上?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a<c<b | C. | c>b>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
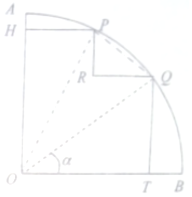 现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com