
 如图,在一条河流的上、下游分别有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.
如图,在一条河流的上、下游分别有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放.| 2×80%+1.4 |
| 700 |
| 3 |
| 700 |
|
| 2×80%+1.4 |
| 700 |
| 3 |
| 700 |
|
|



科目:高中数学 来源: 题型:
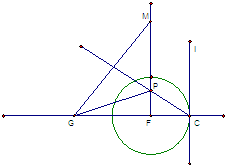 如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知| |PF| |
| d |
| ||
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| GF |
| FC |
| MP |
| PF |
查看答案和解析>>
科目:高中数学 来源: 题型:

| A、31次 | B、32次 |
| C、33次 | D、35次 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为| π |
| 3 |
| PM |
| PF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com