
| A. | $\frac{π}{8}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,求得m的最小值.
解答 解:将函数y=cos4x+sin2x-$\frac{7}{8}$=${(\frac{1+cos2x}{2})}^{2}$+$\frac{1-cos2x}{2}$-$\frac{7}{8}$=$\frac{{cos}^{2}2x}{4}$-$\frac{1}{8}$=$\frac{1+cos4x}{8}$-$\frac{1}{8}$=$\frac{1}{8}$cos4x
的图象向右平移m(m>0)个单位长度后,可得函数y=$\frac{1}{8}$cos4(x-m)=$\frac{1}{8}$cos(4x-4m)的图象,
根据所得到的图象关于原点对称,可得4m=kπ+$\frac{π}{2}$,即 m=$\frac{kπ}{4}$+$\frac{π}{8}$,k∈Z,
则m的最小值为$\frac{π}{8}$,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 与μ,σ有关; | B. | 与μ有关,与σ无关; | ||
| C. | 与σ有关,与μ无关; | D. | 与μ,σ无关. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 15 | 35 | 50 |
| 女生 | 30 | 40 | 70 |
| 总计 | 45 | 75 | 120 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
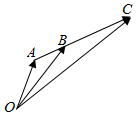 已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)
已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com