
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
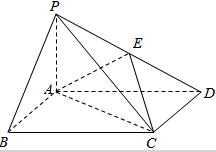 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| 水深(m) | 5.0 | 7.0 | 5.0 | 3.0 | 5.0 | 7.0 | 5.0 | 3.0 | 5.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月消费金额(单位:元) | [0,100) | [100,200) | [200,300) | [300,400) | [400,500) | ≥500 |
| 人数 | 30 | 6 | 9 | 10 | 3 | 2 |
| 高消费 | 非高消费 | 合计 | |
| 男生 | 10 | 20 | 30 |
| 女生 | 5 | 25 | 30 |
| 合计 | 15 | 45 | 60 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 型号 手机品牌 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
| 乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 数学成绩 | 127 | 136 | 137 | 129 | 117 | 129 | 124 | 99 | 108 | 107 | 95 | 107 | 105 | 123 | 113 |
| 地理成绩 | 90 | 72 | 72 | 74 | 70 | 45 | 78 | 62 | 84 | 68 | 76 | 70 | 54 | 76 | 76 |
| 学号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 数学成绩 | 86 | 109 | 84 | 68 | 80 | 69 | 58 | 79 | 58 | 60 | 42 | 71 | 28 | 50 | 40 |
| 地理成绩 | 56 | 66 | 56 | 60 | 40 | 60 | 58 | 50 | 58 | 42 | 56 | 38 | 40 | 44 | 50 |
| 地理Ⅰ | 地理Ⅱ | ||
| 数学Ⅰ | 11 | ||
| 数学Ⅱ | 15 | ||
| 30 |
| P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
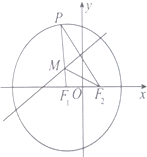 如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.
如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com