
| 学号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 数学成绩 | 127 | 136 | 137 | 129 | 117 | 129 | 124 | 99 | 108 | 107 | 95 | 107 | 105 | 123 | 113 |
| 地理成绩 | 90 | 72 | 72 | 74 | 70 | 45 | 78 | 62 | 84 | 68 | 76 | 70 | 54 | 76 | 76 |
| 学号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 数学成绩 | 86 | 109 | 84 | 68 | 80 | 69 | 58 | 79 | 58 | 60 | 42 | 71 | 28 | 50 | 40 |
| 地理成绩 | 56 | 66 | 56 | 60 | 40 | 60 | 58 | 50 | 58 | 42 | 56 | 38 | 40 | 44 | 50 |
| 地理Ⅰ | 地理Ⅱ | ||
| 数学Ⅰ | 11 | ||
| 数学Ⅱ | 15 | ||
| 30 |
| P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (I)由图表完成2×2列联表,根据列联表中的数据可得K2,和临界值表比对后即可得到答案;
(Ⅱ)数学与地理成绩分属不同层次的同学中共有4人,任取两名枚举可得共有6种情况,抽到的同学数学成绩都为层次I共3种,由古典概型公式,求得抽到的同学数学成绩都为层次I的概率.
解答 解:(I)由题可得如下2×2列联表
| 地理Ⅰ | 地理Ⅱ | 总计 | |
| 数学Ⅰ | 11 | 3 | 14 |
| 数学Ⅱ | 1 | 15 | 16 |
| 总计 | 12 | 18 | 30 |
点评 本题考查独立性检验的应用,考查古典概型公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=$\frac{3}{2}$AC,D是AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=$\frac{3}{2}$AC,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 12 | 20 |
| 合计 | 24 | 16 | 40 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
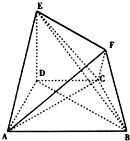 如图,四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2$\sqrt{3}$,DE⊥面ABCD,EF∥BD,且EF=$\frac{2}{3}$BD.
如图,四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2$\sqrt{3}$,DE⊥面ABCD,EF∥BD,且EF=$\frac{2}{3}$BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com