
分析 解:(Ⅰ)代入a=2,根据导数的概念和点斜式求出切线方程即可;
(Ⅱ)构造函数m(x)=$\frac{1}{x}$+lnx,求导函数,根据导函数判断函数的单调性,得出函数的最大值,把零点问题转化为两函数的交点问题求解;
(Ⅲ)由(Ⅱ)知函数的最大值为f(1)=a-1,要使恒成立,只需求出g(x)的最小值即可,利用导函数判断函数的单调性,利用极值得出函数的最值.
解答 解:(Ⅰ)∵a=2,
∴f(1)=2-1=1,
f'(x)=$\frac{1-x}{{x}^{2}}$,
∴f'(1)=0,
∴切线方程为y=1;
(Ⅱ)令m(x)=$\frac{1}{x}$+lnx,
∴m'(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$,
∴当x在(0,1)时,m'(x)>0,m(x)递增,
当x在(1,+∞)是,m'(x)<0,m(x)第减,
故m(x)的最大值为m(1)=1,
f(x)=0恰有一个解,即y=a,与m(x)只有一个交点,
∴a=1;
(Ⅲ)由(Ⅱ)知函数的最大值为f(1)=a-1,
g(x)=ex-ex+1.
g'(x)=ex-e,
∴当x在(0,1)时,g'(x)<0,g(x)递减,
当x在(1,+∞)时,g'(x)>0,g(x)递增,
∴函数g(x)的最小值为g(1)=1,
g(x)≥f(x)恒成立,
∴1≥a-1,
∴a≤2.
点评 考查了导函数的概念,恒成立问题的转化,零点问题的转化,常用方法的应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 学号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 数学成绩 | 127 | 136 | 137 | 129 | 117 | 129 | 124 | 99 | 108 | 107 | 95 | 107 | 105 | 123 | 113 |
| 地理成绩 | 90 | 72 | 72 | 74 | 70 | 45 | 78 | 62 | 84 | 68 | 76 | 70 | 54 | 76 | 76 |
| 学号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 数学成绩 | 86 | 109 | 84 | 68 | 80 | 69 | 58 | 79 | 58 | 60 | 42 | 71 | 28 | 50 | 40 |
| 地理成绩 | 56 | 66 | 56 | 60 | 40 | 60 | 58 | 50 | 58 | 42 | 56 | 38 | 40 | 44 | 50 |
| 地理Ⅰ | 地理Ⅱ | ||
| 数学Ⅰ | 11 | ||
| 数学Ⅱ | 15 | ||
| 30 |
| P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
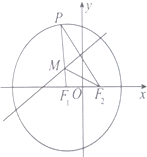 如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.
如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是矩形,AB=8,BC=4,AC与BD相交于O点,P是平面ABCD外一点,PO⊥面ABCD,PO=4,M是PC的中点,求二面角M-BD-C的正切值.
如图,ABCD是矩形,AB=8,BC=4,AC与BD相交于O点,P是平面ABCD外一点,PO⊥面ABCD,PO=4,M是PC的中点,求二面角M-BD-C的正切值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 是否为会员 性别 | 是 | 否 |
| 男生 | 20 | 5 |
| 女生 | 10 | 15 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 70种 | C. | 75种 | D. | 150种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com