
分析 (1)利用绝对值的几何意义,分类讨论,即可解不等式;
(2)求出g(x)=$\sqrt{7x+14}$+$\sqrt{6-x}$的最大值,利用g(x)max>log${\;}_{\sqrt{2}}$(3t+1)成立,求实数t的取值范围.
解答 解:(1)不等式f(x)≥8,即不等式|x+1|+|x-3|≥8,
x<-1时,-x-1-x+3≥8,解得x≤-3,∴x≤-3;
-1≤x≤3时,x+1-x+3≥8,不成立;
x>3时,x+1+x-3≥8,解得x≥5,∴x≥5;
∴不等式f(x)≥8的解集为{x|x≤-3或x≥5};
(2)设$\sqrt{7x+14}$=m,$\sqrt{6-x}$=n,则m2+7n2=56(m≥0,n≥0),
设m=$\sqrt{56}$cosα,n=2$\sqrt{2}$sinα(0≤α≤90°),
∴m+n=2$\sqrt{14}$cosα+2$\sqrt{2}$sinα=8sin(α+θ),
∴(m+n)max=8,
∵存在实数x0,使得g(x0)>log${\;}_{\sqrt{2}}$(3t+1)成立,
∴8>log${\;}_{\sqrt{2}}$(3t+1),
∴0<3t+1<$(\sqrt{2})^{8}$,
∴-$\frac{1}{3}$<t<5.
点评 本题考查不等式的解法,考查分类讨论的数学思想,考查函数的最值,正确求出函数的最大值是关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $0<m≤\frac{1}{3}$ | B. | $0<m<\frac{1}{2}$ | C. | $\frac{1}{2}<m≤1$ | D. | $\frac{1}{3}<m<1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
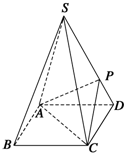 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 态度 | 积极支持企业改革 | 不太支持企业改革 | 总计 |
| 工作积极 | 54 | 40 | 94 |
| 工作一般 | 32 | 63 | 95 |
| 总计 | 86 | 103 | 189 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com