
分析 (1)求出函数的导数,根据$g'(-\frac{1}{2})=\frac{3}{4}$,求出a的值,图象C过点$A(-\frac{1}{2},\frac{3}{4})$,求出b的值,问题转化为证明当x∈(-∞,2]时,$\frac{3}{4}x+\frac{9}{8}≥g(x)$,根据函数的单调性证明即可;
(2)问题转化为证明?x∈(-∞,2],$f(x)≥\frac{3}{4}x+\frac{9}{8}$,构造函数g(x),根据函数的单调性证明即可.
解答 解:(1)g'(x)=3ax2-2x-1,
因为g(x)=ax3-x2-x+b的图象C在$x=-\frac{1}{2}$处的切线方程是$y=\frac{3}{4}x+\frac{9}{8}$,
所以$g'(-\frac{1}{2})=\frac{3}{4}$,即$3a{(-\frac{1}{2})^2}-2×(-\frac{1}{2})-1=\frac{3}{4}$,解得a=1.
因为图象C过点$A(-\frac{1}{2},\frac{3}{4})$,所以${(-\frac{1}{2})^3}-{(-\frac{1}{2})^2}-(-\frac{1}{2})+b=\frac{3}{4}$,解得$b=\frac{5}{8}$.
要证明:当x∈(-∞,2]时,g(x)的图象C上任意一点都在切线$y=\frac{3}{4}x+\frac{9}{8}$上或在其下方,
只要证明:当x∈(-∞,2]时,$\frac{3}{4}x+\frac{9}{8}≥g(x)$.
令$k(x)=\frac{3}{4}x+\frac{9}{8}-g(x)=-{x^3}+{x^2}+\frac{7}{4}x+\frac{1}{2}$,
$k'(x)=-3{x^x}+2x+\frac{7}{4}$,令$k'(x)=-3{x^x}+2x+\frac{7}{4}=0$,得$x=-\frac{1}{2},x=\frac{7}{6}$,
验证得$k{(x)_{min}}=min\left\{{k(-\frac{1}{2}),k(2)}\right\}=0$,
所以?x∈(-∞,2],$\frac{3}{4}x+\frac{9}{8}≥g(x)$成立,
所以当x∈(-∞,2]时,g(x)的图象C上任意一点都在切线$y=\frac{3}{4}x+\frac{9}{8}$上或在其下方.
(2)只要证明:?x∈(-∞,2],$f(x)≥\frac{3}{4}x+\frac{9}{8}$.
?x∈(-∞,2],令$h(x)=f(x)-(\frac{3}{4}x+\frac{9}{8})=\frac{3}{4}{e^{x+\frac{1}{2}}}-\frac{3}{4}x-\frac{9}{8}$,
$h'(x)=\frac{3}{4}{e^{x+\frac{1}{2}}}-\frac{3}{4}$,令$h'(x)=0,x=-\frac{1}{2}$,
当$x∈(-∞,-\frac{1}{2})$时,h'(x)<0,当$x∈(-\frac{1}{2},2)$时,h'(x)>0,所以$h(x)≥h(-\frac{1}{2})=0$,
所以?x∈(-∞,2],$f(x)≥\frac{3}{4}x+\frac{9}{8}$成立,
又由(1)得,?x∈(-∞,2],$\frac{3}{4}x+\frac{9}{8}≥g(x)$,
所以?x∈(-∞,2],$f(x)≥\frac{3}{4}x+\frac{9}{8}≥g(x)$,
所以?x∈(-∞,2],f(x)≥g(x).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,考查转化思想,是一道综合题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
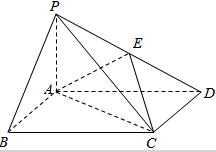 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 型号 手机品牌 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
| 乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 数学成绩 | 127 | 136 | 137 | 129 | 117 | 129 | 124 | 99 | 108 | 107 | 95 | 107 | 105 | 123 | 113 |
| 地理成绩 | 90 | 72 | 72 | 74 | 70 | 45 | 78 | 62 | 84 | 68 | 76 | 70 | 54 | 76 | 76 |
| 学号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 数学成绩 | 86 | 109 | 84 | 68 | 80 | 69 | 58 | 79 | 58 | 60 | 42 | 71 | 28 | 50 | 40 |
| 地理成绩 | 56 | 66 | 56 | 60 | 40 | 60 | 58 | 50 | 58 | 42 | 56 | 38 | 40 | 44 | 50 |
| 地理Ⅰ | 地理Ⅱ | ||
| 数学Ⅰ | 11 | ||
| 数学Ⅱ | 15 | ||
| 30 |
| P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
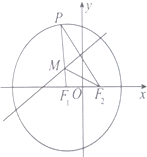 如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.
如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com