
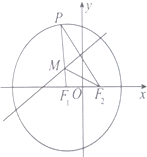
 如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.
如图,已知P是以F1(-1,0)为圆心,以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.分析 (Ⅰ)设M(x,y),M在线段PF2的垂直平分线上,|MP|=|MF2|,可得|MF1|+|MF2|=|MF1|+|MP|=4>|F1F2|.M的轨迹为以F1,F2为焦点的椭圆,设椭圆的方程$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,由题意可求得a、b的值,求得椭圆方程;
(Ⅱ)(ⅰ)设出直线AB的方程,将直线方程代入椭圆方程,得到关于x的一元二次方程,由韦达定理求得x1+x2及x1•x2,分别求得kAE及kBE,由kAE+kBE=0,即可求得∠AEF2=∠BEF2;
(ⅱ)由cos∠AEB=$\frac{7}{9}$,求得tan∠AEB,由$\frac{y_1}{{{x_1}-4}}=-\frac{{\sqrt{2}}}{4}$,
解答 解:(Ⅰ)设M(x,y),则因为M在线段PF2的垂直平分线上,
所以|MP|=|MF2|,
所以|MF1|+|MF2|=|MF1|+|MP|=4>|F1F2|.
即M的轨迹为以F1,F2为焦点的椭圆,…(2分)
其长半轴为a=2,半焦距为c=1,
所以短半轴$b=\sqrt{{a^2}-{c^2}}=\sqrt{3}$.
所以C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(Ⅱ)(ⅰ)证明:设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-1),
则$\left\{\begin{array}{l}3{x^2}+4{y^2}=12\\ y=k(x-1)\end{array}\right.\;⇒(3+4{k^2}){x^2}-8{k^2}x+4{k^2}-12=0$,
${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$.
则${k_{AE}}=\frac{y_1}{{{x_1}-4}}$,${k_{BE}}=\frac{y_2}{{{x_2}-4}}$.…(6分)
所以${k_{AE}}+{k_{BE}}=\;\;\frac{y_1}{{{x_1}-4}}\;+\frac{y_2}{{{x_2}-4}}\;=\frac{{k({x_1}-1)}}{{{x_1}-4}}\;+\frac{{k({x_2}-1)}}{{{x_2}-4}}$,
=$\frac{{k({x_1}-1)({x_2}-4)+k({x_2}-1)({x_1}-4)}}{{({x_1}-4)({x_2}-4)}}=\;\;\frac{{k[2{x_1}{x_2}-5({x_1}+{x_2})+8]}}{{({x_1}-4)({x_2}-4)}}=0$.
即∠AEF2=∠BEF2.…(8分)
(ⅱ)因为$cos∠AEB=\frac{7}{9}$,
所以$tan∠AE{F_2}=tan∠BE{F_2}=\frac{{\sqrt{2}}}{4}$,不妨设点A在第一象限,
则$\frac{y_1}{{{x_1}-4}}=-\frac{{\sqrt{2}}}{4}$,$\frac{y_2}{{{x_2}-4}}=\frac{{\sqrt{2}}}{4}$,
所以$\frac{{{y_1}^2}}{{{{({x_1}-4)}^2}}}=\frac{1}{8}$,$\frac{{{y_2}^2}}{{{{({x_2}-4)}^2}}}\;=\frac{1}{8}$;
即$\left\{\begin{array}{l}{({x_1}-4)^2}=8{y_1}^2\\{({x_2}-4)^2}=8{y_2}^2\end{array}\right.$,$\left\{\begin{array}{l}{({x_1}-4)^2}=8•3(1-\frac{{{x_1}^2}}{4})\\{({x_2}-4)^2}=8•3(1-\frac{{{x_2}^2}}{4})\end{array}\right.$…(10分)
所以x1,x2是方程${(x-4)^2}=8•3(1-\frac{x^2}{4})$,
即方程7x2-8x-8=0的两个根,
所以${x_1}+{x_2}=\frac{8}{7}$,${x_1}{x_2}=-\frac{8}{7}$,
所以$\frac{{8{k^2}}}{{3+4{k^2}}}=\frac{8}{7}$,k2=1.又倾斜角为锐角,
所以k>0,所以直线AB的方程为y=x-1.…(12分)
点评 本题考查椭圆标准方程的求法、直线与椭圆的位置关系及其应用,韦达定理及弦长公式,考查转化思想及运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
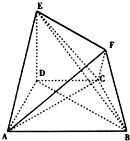 如图,四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2$\sqrt{3}$,DE⊥面ABCD,EF∥BD,且EF=$\frac{2}{3}$BD.
如图,四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2$\sqrt{3}$,DE⊥面ABCD,EF∥BD,且EF=$\frac{2}{3}$BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
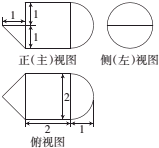
| A. | $\frac{17π}{6}$ | B. | $\frac{17π}{3}$ | C. | 5π | D. | $\frac{13π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 态度 | 积极支持企业改革 | 不太支持企业改革 | 总计 |
| 工作积极 | 54 | 40 | 94 |
| 工作一般 | 32 | 63 | 95 |
| 总计 | 86 | 103 | 189 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com