
 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=$\frac{3}{2}$AC,D是AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=$\frac{3}{2}$AC,D是AC的中点.分析 (1)取A1C1的中点E,以D为原点,DC为x轴,DB为y轴,DE为z轴,建立空间直角坐标系,利用向量法能求出点B1到平面A1BD的距离.
(2)求出平面A1BD的法向量和平面AA1B的法向量,利用向量法能求出二面角A-A1B-D的余弦值.
解答 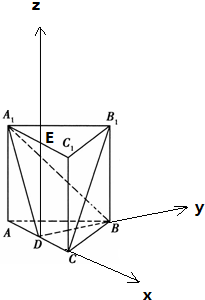 解:(1)取A1C1的中点E,连结DE,
解:(1)取A1C1的中点E,连结DE,
∵在直三棱柱ABC-A1B1C1中,AA1=AB=BC=$\frac{3}{2}$AC,D是AC的中点,
∴DE⊥平面ABC,BD⊥AC,
以D为原点,DC为x轴,DB为y轴,DE为z轴,建立空间直角坐标系,
设AA1=AB=BC=$\frac{3}{2}$AC=3,
则B1(0,2$\sqrt{2}$,3),A1(-1,0,3),D(0,0,0),B(0,2$\sqrt{2}$,0),
$\overrightarrow{D{B}_{1}}$=(0,2$\sqrt{2}$,3),$\overrightarrow{D{A}_{1}}$=(-1,0,3),$\overrightarrow{DB}$=(0,2$\sqrt{2}$,0),
设平面A1BD的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{D{A}_{1}}=-x+3z=0}\\{\overrightarrow{n}•\overrightarrow{DB}=2\sqrt{2}y=0}\end{array}\right.$,取x=3,得$\overrightarrow{n}$=(3,0,1),
∴点B1到平面A1BD的距离d=$\frac{|\overrightarrow{D{B}_{1}}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{3}{\sqrt{17}•\sqrt{10}}$=$\frac{3\sqrt{170}}{170}$.
(2)平面A1BD的法向量$\overrightarrow{n}$=(3,0,1),
设平面AA1B的法向量$\overrightarrow{m}$=(a,b,c),
A(-1,0,0),$\overrightarrow{A{A}_{1}}$=(0,0,3),$\overrightarrow{AB}$=(1,2$\sqrt{2}$,0),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{A{A}_{1}}=3c=0}\\{\overrightarrow{m}•\overrightarrow{AB}=a+2\sqrt{2}b=0}\end{array}\right.$,取a=2$\sqrt{2}$,得b=-1,∴$\overrightarrow{m}$=(2$\sqrt{2}$,-1,0),
设二面角A-A1B-D的平面角为θ,
cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{6\sqrt{2}}{\sqrt{10}•\sqrt{9}}$=$\frac{2\sqrt{5}}{5}$.
∴二面角A-A1B-D的余弦值为$\frac{2\sqrt{5}}{5}$.
点评 本题考查点到平面的距离的求法,考查二面角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
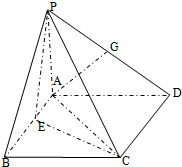 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
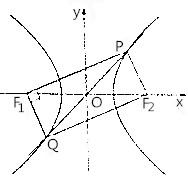 如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )
如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )| A. | 2+$\sqrt{2}$ | B. | 2+$\sqrt{6}$ | C. | $\sqrt{2+\sqrt{2}}$ | D. | $\sqrt{2+\sqrt{6}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
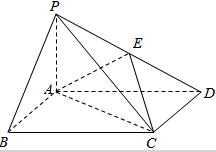 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 数学成绩 | 127 | 136 | 137 | 129 | 117 | 129 | 124 | 99 | 108 | 107 | 95 | 107 | 105 | 123 | 113 |
| 地理成绩 | 90 | 72 | 72 | 74 | 70 | 45 | 78 | 62 | 84 | 68 | 76 | 70 | 54 | 76 | 76 |
| 学号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 数学成绩 | 86 | 109 | 84 | 68 | 80 | 69 | 58 | 79 | 58 | 60 | 42 | 71 | 28 | 50 | 40 |
| 地理成绩 | 56 | 66 | 56 | 60 | 40 | 60 | 58 | 50 | 58 | 42 | 56 | 38 | 40 | 44 | 50 |
| 地理Ⅰ | 地理Ⅱ | ||
| 数学Ⅰ | 11 | ||
| 数学Ⅱ | 15 | ||
| 30 |
| P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com