Question

14．已知O为坐标原点，A，B两点的坐标均满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≤0}\\{x-1≥0}\end{array}\right.$则tan∠AOB的最大值等于$\frac{3}{4}$．

Answer 1

分析 先根据约束条件画出可行域，只需求出A，B在图中的位置，∠AOB最大，即tan∠AOB最大即可．

解答 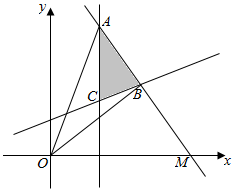解：作出可行域，则A、B在图中所示的位置时，∠AOB最大，即tan∠AOB最大，
由题意可得A（1，2），B（2，1）
∴K_OA=tan∠AOM=2，K_OB=tan∠BOM=$\frac{1}{2}$
∵∠AOB=∠AOM-∠BOM，
∴tan∠AOB=tan（∠AOM-∠BOM）
=$\frac{tan∠AOM-tan∠BOM}{1+tan∠AOMtan∠BOM}$
=$\frac{2-\frac{1}{2}}{1+2×\frac{1}{2}}$=$\frac{3}{4}$，
所以tan∠AOB的最大值为$\frac{3}{4}$，
故答案为：$\frac{3}{4}$．

点评 借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．线性规划中的最优解，通常是利用平移直线法确定．巧妙识别目标函数的几何意义是我们研究规划问题的基础．