
分析 由二项式定理和排列组合的知识列出关于a的方程,解方程即可.
解答 解:(2x-ay)2(x+y)6的展开式中含x3y5项,
由第一个因式中2个x和第二个因式中1个x,5个y相乘,
第一个因式中1个x,1个y和第二个因式中2个x,4个y相乘,
第一个因式中2个y和第二个因式中3个x,3个y相乘,再把所得的积相加得到的;
∴x3y5的系数为:
22•${C}_{6}^{5}$+${C}_{2}^{1}$•2•(-a)•${C}_{6}^{4}$+(-a)2•${C}_{6}^{3}$=24-60a+20a2=-16,
整理得a2-3a+2=0,
解得a=1或a=2,
故答案为:1或2.
点评 本题考查了二项式定理的应用问题,涉及了排列组合知识的应用问题,是基础题目.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{10}$,5 | B. | 40,5 | C. | 2$\sqrt{10}$,3 | D. | 40,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7\sqrt{2}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 109 | B. | 101 | C. | -107 | D. | -109 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
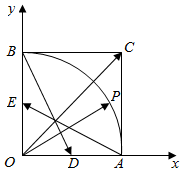 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )| A. | -$\sqrt{2}$ | B. | -2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com