Question

1．如图l是某县参加2016年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A₁、A₂、
…、A_m（如A₂表示身高（单位：cm）在[150，155）内的学生人数）．图2是统计图l中身高在一定范围内学生人数的一个算法流程图．根据流程图中输出的S值是1850．

Answer 1

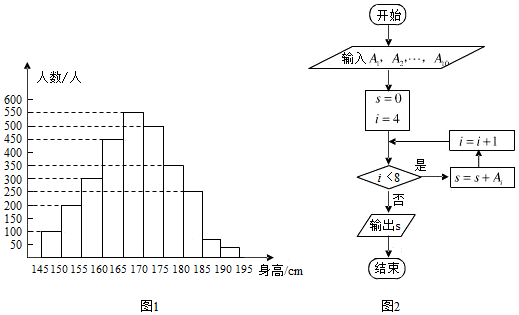
分析 由题目要求可知：该程序的作用是统计身高在160～180cm（含160cm，不含180cm））的学生人数，由图1可知第四组数据到第七组数据是值，相加求和即可．

解答 解：模拟图2中程序的运行，可得其功能是要统计并输出：
身高在160-180cm之间的学生的人数，
即是要计算并输出s=A₄+A₅+A₆+A₇的值，
由图1可得：A₄=450，A₅=550，A₆=500，A₇=350，
故根据流程图中输出的s=A₄+A₅+A₆+A₇=1850．
故答案为：1850．

点评 本题考查了算法与程序图框的应用问题，也考查了频率分布直方图的应用问题，解题时应准确理解算法程序的意义，把统计与框图两部分内容进行交汇考查，体现了考题设计上的新颖，突出了新课标高考中对创新能力的考查要求，属于基础题．