
| A. | 4xf(x2)≤x4f(2x) | B. | e2xf($\frac{1}{x}$)≥$\frac{1}{{x}^{2}}$f(ex) | ||
| C. | xf($\sqrt{x}$)≤f(x) | D. | 4xf(x+1)≤(x2+2x+1)f(2$\sqrt{x}$) |
分析 x>0时,可得2xf(x)-x2f′(x)>x2>0,令g(x)=$\frac{{x}^{2}}{f(x)}$,则f′(x)=$\frac{2xf(x)-{x}^{2}f′(x)}{{f}^{2}(x)}$>0.即函数g(x)在(0,+∞)单调递增,可得g(x+1)≥g(2$\sqrt{x}$),即可得到结论.
解答 解:当x>0时,有2f(x)>xf′(x)+x恒成立,⇒有2xf(x)-x2f′(x)>x2>0,
令g(x)=$\frac{{x}^{2}}{f(x)}$,则f′(x)=$\frac{2xf(x)-{x}^{2}f′(x)}{{f}^{2}(x)}$>0.
∴函数g(x)在(0,+∞)单调递增,
∵x>0,∴$x+1≥2\sqrt{x}$,即g(x+1)≥g(2$\sqrt{x}$)
⇒$\frac{(x+1)^{2}}{f(x+1)}≥\frac{(2\sqrt{x})^{2}}{f(2\sqrt{x})}$,∵f(x)>0恒成立.∴f(x+1)>0,f(2$\sqrt{x}$)>0,
∴(x+1)2f(2$\sqrt{x}$)≥4xf(x+1).
故选:D.
点评 本题考查了构造新函数,解函数不等式,属于中档题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{27}$ | B. | $\frac{2}{27}$ | C. | $\frac{2}{81}$ | D. | $\frac{8}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{3π}{16},\frac{11π}{16})$ | B. | $(\frac{π}{16},\frac{9π}{16})$ | C. | $(-\frac{3π}{16},\frac{5π}{16})$ | D. | $(\frac{π}{16},\frac{5π}{16})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
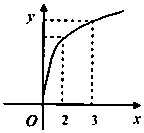 函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f′(3)<f(3)-f(2)<f′(2) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f(3)-f(2)<f′(2)<f′(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com