
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值即可;
(Ⅱ)根据函数的单调性得到函数的最小值,从而求出a的范围即可.
解答 解:(Ⅰ)f′(x)=lnx+1,
令f′(x)<0,解得:0<x<$\frac{1}{e}$,
令f′(x)>0,解得:x>$\frac{1}{e}$,
故f(x)在(0,$\frac{1}{e}$)递减,在($\frac{1}{e}$,e]递增;
故f(x)极小值=f($\frac{1}{e}$)=-$\frac{1}{e}$;
(Ⅱ)由(Ⅰ)得:x∈(0,e]时,f(x)min=-$\frac{1}{e}$,
故a≥-$\frac{1}{e}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
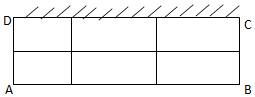 某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?
某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4xf(x2)≤x4f(2x) | B. | e2xf($\frac{1}{x}$)≥$\frac{1}{{x}^{2}}$f(ex) | ||
| C. | xf($\sqrt{x}$)≤f(x) | D. | 4xf(x+1)≤(x2+2x+1)f(2$\sqrt{x}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4033 | B. | 4033 | C. | 8066 | D. | -8066 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}+4ln2$ | B. | 4(1-ln2) | C. | 2(1-ln2) | D. | 4(2ln2-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com