
分析 由f(x+a)的关系式,将x换为x+a,可得f(x+2a),再将x换为x+2a,可得f(x+4a)=f(x),由周期函数的定义,即可得到所求周期.
解答 解:函数y=f(x)满足$f({x+a})=\frac{1+f(x)}{1-f(x)}$,x∈R,
可得f(x+2a)=$\frac{1+f(x+a)}{1-f(x+a)}$=$\frac{1+\frac{1+f(x)}{1-f(x)}}{1-\frac{1+f(x)}{1-f(x)}}$=$\frac{2}{-2f(x)}$=-$\frac{1}{f(x)}$,
即有f(x+4a)=-$\frac{1}{f(x+2a)}$=f(x),
则函数y=f(x)的最小正周期为4|a|.
故答案为:4|a|.
点评 本题考查函数的周期的求法,注意运用周期函数的定义,以及赋值法,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{3π}{16},\frac{11π}{16})$ | B. | $(\frac{π}{16},\frac{9π}{16})$ | C. | $(-\frac{3π}{16},\frac{5π}{16})$ | D. | $(\frac{π}{16},\frac{5π}{16})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
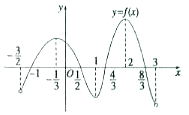 函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
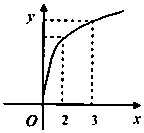 函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f′(3)<f(3)-f(2)<f′(2) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f(3)-f(2)<f′(2)<f′(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com