
| A. | $(\frac{3π}{16},\frac{11π}{16})$ | B. | $(\frac{π}{16},\frac{9π}{16})$ | C. | $(-\frac{3π}{16},\frac{5π}{16})$ | D. | $(\frac{π}{16},\frac{5π}{16})$ |
分析 由题意求得φ=$\frac{π}{8}$,可得f(x)=-2tan(2x+$\frac{π}{8}$),令kπ-$\frac{π}{2}$<2x+$\frac{π}{8}$<kπ+$\frac{π}{2}$,求得x的范围,可得函数的减区间.
解答 解:∵函数f(x)=-2tan(2x+φ)(|φ|<π),若$f(\frac{π}{16})=-2$=-2tan($\frac{π}{8}$+φ),
∴tan($\frac{π}{8}$+φ)=1,∴φ=$\frac{π}{8}$,f(x)=-2tan(2x+$\frac{π}{8}$),令kπ-$\frac{π}{2}$<2x+$\frac{π}{8}$<kπ+$\frac{π}{2}$,
求得$\frac{kπ}{2}$-$\frac{5π}{16}$<x<$\frac{kπ}{2}$+$\frac{3π}{16}$,可得f(x)的单调递减区间为( $\frac{kπ}{2}$-$\frac{5π}{16}$,$\frac{kπ}{2}$+$\frac{3π}{16}$),k∈Z.
令k=1,可得f(x)的一个单调递减区间是($\frac{3π}{16}$,$\frac{11π}{16}$),
故选:A.
点评 本题主要考查正切函数的单调性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | .2 | B. | .$-\frac{1}{e^2}-1$ | C. | .$-\frac{1}{e^2}+1$ | D. | 2-e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
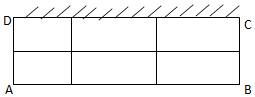 某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?
某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4xf(x2)≤x4f(2x) | B. | e2xf($\frac{1}{x}$)≥$\frac{1}{{x}^{2}}$f(ex) | ||
| C. | xf($\sqrt{x}$)≤f(x) | D. | 4xf(x+1)≤(x2+2x+1)f(2$\sqrt{x}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com