练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．在所有的两位数中，十位数字大于个位数字的两位数共有（　　）
    A．50B．45C．36D．35

    分析 根据题意，按个位数字的不同分9种情况讨论，分别求出每一种情况的符合条件的两位数数目，由分类计数原理计算可得答案．

    解答 解：根据题意，按个位数字的不同分9种情况讨论：
    ①、当个位数字为0时，其十位数字可以为1、2、3、4、5、6、7、8、9，共9种情况；
    ②、当个位数字为1时，其十位数字可以为2、3、4、5、6、7、8、9，共8种情况；
    ③、当个位数字为2时，其十位数字可以为3、4、5、6、7、8、9，共7种情况；
    ④、当个位数字为3时，其十位数字可以为4、5、6、7、8、9，共6种情况；
    ⑤、当个位数字为4时，其十位数字可以为5、6、7、8、9，共5种情况；
    ⑥、当个位数字为5时，其十位数字可以为6、7、8、9，共4种情况；
    ⑦、当个位数字为6时，其十位数字可以为7、8、9，共3种情况；
    ⑧、当个位数字为7时，其十位数字可以为8、9，共2种情况；
    ⑨、当个位数字为8时，其十位数字可以为9，共1种情况；
    则十位数字大于个位数字的两位数共有9+8+7+6+5+4+3+2+1=45个；
    故答案为：45．

    点评 本题考查分类计数原理的应用，注意“十位数字大于个位数字”与“十位数字小于个位数字”的个数不等，不能用倍分法分析．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）=-2tan（2x+φ）（|φ|＜π），若$f（\frac{π}{16}）=-2$，则f（x）的一个单调递减区间是（　　）
    A．$（\frac{3π}{16}，\frac{11π}{16}）$B．$（\frac{π}{16}，\frac{9π}{16}）$C．$（-\frac{3π}{16}，\frac{5π}{16}）$D．$（\frac{π}{16}，\frac{5π}{16}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

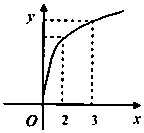    4．函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（　　）
    A．0＜f′（2）＜f′（3）＜f（3）-f（2）B．0＜f′（3）＜f（3）-f（2）＜f′（2）C．0＜f′（3）＜f′（2）＜f（3）-f（2）D．0＜f（3）-f（2）＜f′（2）＜f′（3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．复数z在眏射f下的象为（2+i）z，则1-2i的原象为（　　）
    A．-iB．iC．4-3iD．4+3i

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．下表数据为某地区某基地某种农产品的年产量x（单位：吨）及对应销售价格y（单位：万元/吨）．
    x123
    y543
    （1）若y与x有较强的线性相关关系，请用最小二乘法求出y关与x的线性回归方程$\widehaty=\widehatbx+\widehata$；
    （2）若每吨该农产品的成本为1万元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润z最大？最大利润是多少？
    参考公式：$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{（{{x_i}{y_i}}）}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=4cosωxsin（ωx-$\frac{π}{6}$）（ω＞0）的最小正周期是π．
    （1）求函数f（x）在区间x∈（0，π）的单调递增区间；
    （2）求f（x）在$[{\frac{π}{6}，\frac{2π}{3}}]$上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设正实数x，y满足x+2y=xy，若m2+2m＜x+2y恒成立，则实数m的取值范围是（-4，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知$sin（α-\frac{3π}{2}）＜0，tanα＜0$，则角α是第二象限角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=x3+ax2+bx在x=-1与x=2处都取得极值．
    （Ⅰ）求a，b的值及函数f（x）的单调区间；
    （Ⅱ）若x∈[-2，3]时，f（x）＜m恒成立，求m的取值范围．

    查看答案和解析>>

    同步练习册答案