
分析 (1)根据向量的数量积的运算和两角和的正弦公式化简f(x)=$2sin(x+\frac{π}{6})-1$,再代值计算即可,
(2)根据正弦函数的图象和性质即可求出单调区间和最值.
解答 解:(1)∵$\overrightarrow a=(1,\sqrt{3})$,$\overrightarrow b=(cosx,sinx)$,
∴$f(x)=\overrightarrow a•\overrightarrow b-1=cosx+\sqrt{3}sinx-1$=$2sin(x+\frac{π}{6})-1$
令f(x)=0,则$x+\frac{π}{6}=\frac{π}{6}+2kπ$或$x+\frac{π}{6}=\frac{5π}{6}+2kπ$,k∈Z,
∴x=2kπ或$x=\frac{2π}{3}+2kπ$,k∈Z
∴{x|x=2kπ或$x=\frac{2π}{3}+2kπ$,k∈Z}.
(2)由-$\frac{π}{2}$+2kπ≤x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,由$\frac{π}{2}$+2kπ≤x+$\frac{π}{6}$≤$\frac{3}{2}$π+2kπ,k∈Z,
即-$\frac{2}{3}$π+2kπ≤x≤$\frac{π}{3}$+2kπ,k∈Z,$\frac{π}{3}$+2kπ≤x≤$\frac{4}{3}$π+2kπ,k∈Z
∵x∈[0,$\frac{π}{2}$]
∴f(x)在[0,$\frac{π}{3}$]上单调递增,在[$\frac{π}{3}$,$\frac{π}{2}$]
即-$\frac{2}{3}$π+2kπ≤x≤$\frac{π}{3}$+2kπ,k∈Z,
∵$x∈[0,\frac{π}{2}]$,∴$x+\frac{π}{6}∈[\frac{π}{6},\frac{2π}{3}]$,
∴$sin(x+\frac{π}{6})∈[\frac{1}{2},1]$,
∴f(x)∈[0,1].
∴f(x)的最大值为1,最小值为0
点评 本题考查了向量的数量积,以及三角函数的恒等变化以及正弦函数的图象和性质,属于中档题


科目:高中数学 来源: 题型:填空题
 将全体正整数ai,j从左向右排成一个直角三角形数阵:
将全体正整数ai,j从左向右排成一个直角三角形数阵:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{3π}{16},\frac{11π}{16})$ | B. | $(\frac{π}{16},\frac{9π}{16})$ | C. | $(-\frac{3π}{16},\frac{5π}{16})$ | D. | $(\frac{π}{16},\frac{5π}{16})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{8}^{4}$C${\;}_{4}^{2}$C${\;}_{2}^{2}$ | B. | C${\;}_{3}^{1}$C${\;}_{8}^{2}$ | ||
| C. | $\frac{{C}_{8}^{4}{C}_{4}^{2}}{{A}_{2}^{2}}$ | D. | $\frac{{C}_{8}^{4}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{3}^{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
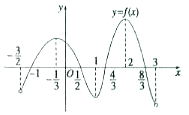 函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com