
 将全体正整数ai,j从左向右排成一个直角三角形数阵:
将全体正整数ai,j从左向右排成一个直角三角形数阵:科目:高中数学 来源: 题型:解答题
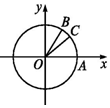 在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.
在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
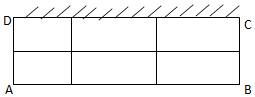 某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?
某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4033 | B. | 4033 | C. | 8066 | D. | -8066 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com