
���� ��1��ֱ��l�IJ���������ȥ����t�����ֱ��l��ֱ�����귽�̣�����C�ļ����귽�̻�Ϊ��2=2��cos�ȣ��ɴ����������C����ͨ���̣�
��2������C��ֱ�����귽��Ϊ��x-1��2+y2=1����ֱ�����������飬�ɴ������ֱ��l������C�Ľ����ֱ�����꣮
��� �⣺��1����Ϊֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{3}t\\ y=t-\sqrt{3}\end{array}\right.$��
��$t=y+\sqrt{3}$������$x=\frac{{\sqrt{3}}}{3}t$��
��$3x-\sqrt{3}y=3$����$\sqrt{3}x-y-\sqrt{3}=0$��
��ֱ��l��ֱ�����귽��Ϊ$\sqrt{3}x-y-\sqrt{3}=0$��
������C�ļ����귽��Ϊ��=2cos�ȣ����2=2��cos�ȣ�
������C����ͨ����x2+y2=2x����x2-2x+y2=0��
��2������C��ֱ�����귽��Ϊ��x-1��2+y2=1��
��$\left\{\begin{array}{l}\sqrt{3}x-y-\sqrt{3}=0\\{��{x-1}��^2}+{y^2}=1\end{array}\right.$�����$\left\{\begin{array}{l}x=\frac{3}{2}\\ y=\frac{{\sqrt{3}}}{2}\end{array}\right.$��$\left\{\begin{array}{l}x=\frac{1}{2}\\ y=-\frac{{\sqrt{3}}}{2}\end{array}\right.$��
��ֱ��l������C�Ľ����ֱ������Ϊ$��{\frac{3}{2}��\frac{{\sqrt{3}}}{2}}������{\frac{1}{2}��-\frac{{\sqrt{3}}}{2}}��$��
���� ���⿼��ֱ�ߵ�ֱ�����귽�̡����ߵ���ͨ���̵�������ֱ�������ߵĽ����ֱ����������漰�������귽�̡��������̡�ֱ�����귽�̵Ļ����Ȼ���֪ʶ������������֤����������������������黯����ת��˼�롢�����뷽��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ȫ��������ai��j���������ų�һ��ֱ������������
��ȫ��������ai��j���������ų�һ��ֱ�������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
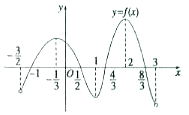 ����y=f��x�����䶨����$[{-\frac{3}{2}��3}]$�ڿɵ�����ͼ����ͼ��ʾ����y=f��x���ĵ�����Ϊy=f'��x������ʽf�䣨x����0�Ľ⼯��[-$\frac{1}{3}$��1]��[2��3����
����y=f��x�����䶨����$[{-\frac{3}{2}��3}]$�ڿɵ�����ͼ����ͼ��ʾ����y=f��x���ĵ�����Ϊy=f'��x������ʽf�䣨x����0�Ľ⼯��[-$\frac{1}{3}$��1]��[2��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $x+2y+\sqrt{5}=0$��$x+2y-\sqrt{5}=0$ | B�� | $x-2y+\sqrt{5}=0$��$x-2y-\sqrt{5}=0$ | ||
| C�� | x+2y+5=0��x+2y-5=0 | D�� | x-2y+5=0��x-2y-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -i | B�� | i | C�� | 4-3i | D�� | 4+3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com