
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,由余弦定理可得cosaA,即可判定;
②,若a2+b2>c2,只能判定C为锐角,不能判定△ABC为锐角三角形;
③,由正弦定理得a:b:c=sinA:sinB:sinC≠A:B:C;
④,由题意判断出三角形有两解时,A的范围,通过正弦定理及正弦函数的性质推出a的范围即可.
解答 解:对于①,由余弦定理得cosA=$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{2bc}=-\frac{1}{2}$,∴A=120°,故错;
对于②,若a2+b2>c2,只能判定C为锐角,不能判定△ABC为锐角三角形,故错;
对于③,由正弦定理得a:b:c=sinA:sinB:sinC≠A:B:C,故错;
对于④,解:由AC=b=2,要使三角形有两解,就是要使以C为圆心,半径为2的圆与BA有两个交点,
当A=90°时,圆与AB相切;当A=45°时交于B点,也就是只有一解,
∴45°<A<135°,且A≠90°,即$\frac{\sqrt{2}}{2}$<sinA<1,由正弦定理以及asinB=bsinA.可得:a=$\frac{bsinA}{sinB}$
=2$\sqrt{2}$sinA,∵2$\sqrt{2}$sinA∈(2,2$\sqrt{2}$).∴a的取值范围是(2,2$\sqrt{2}$).故正确.
故选:A
点评 本题考查了命题的真假判定,涉及到了解三角形的基础知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
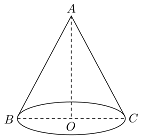 已知圆锥的侧面展开图是一个半圆;
已知圆锥的侧面展开图是一个半圆;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .2 | B. | .$-\frac{1}{e^2}-1$ | C. | .$-\frac{1}{e^2}+1$ | D. | 2-e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4xf(x2)≤x4f(2x) | B. | e2xf($\frac{1}{x}$)≥$\frac{1}{{x}^{2}}$f(ex) | ||
| C. | xf($\sqrt{x}$)≤f(x) | D. | 4xf(x+1)≤(x2+2x+1)f(2$\sqrt{x}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com