
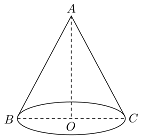
 已知圆锥的侧面展开图是一个半圆;
已知圆锥的侧面展开图是一个半圆;分析 (1)根据侧面展开图的特征列方程得出底面半径和母线的关系,从而得出母线与底面所成的角;
(2)根据抛物线的一条弦为圆锥底面直径得出底面半径和p的关系,从而可得圆锥的面积;
(3)利用三角形相似和圆锥的特点得出椭圆的长轴,短轴和底面半径的关系,从而可得长短轴的关系,得出答案.
解答 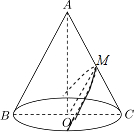 解:(1)设圆锥的底面半径为r,母线长为l,
解:(1)设圆锥的底面半径为r,母线长为l,
则圆锥侧面展开图的半径为l,弧长为2πr,
∵圆锥的侧面展开图是一个半圆,∴2πr=πl,
∴l=2r,∴圆锥的轴截面为等边三角形,
∴圆锥的母线与底面所成的角为$\frac{π}{3}$.
(2)设抛物线的顶点M,则M为AC的中点,
设抛物线方程为y2=2px,把y=r代入抛物线方程得x=$\frac{{r}^{2}}{2p}$,
∴OM=$\frac{{r}^{2}}{2p}$,于是母线l=AB=2OM=$\frac{{r}^{2}}{p}$,
又由(1)可知l=2r,即$\frac{{r}^{2}}{p}$=2r,∴r=2p,l=4p,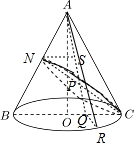
∴圆锥的全面积为πr2+πrl=12πp2.
(3)设AB的中点为N,则N和C为椭圆的长轴顶点,
取CN的中点P,则P为椭圆的中心,连接AP并延长,交BC于Q,过Q作QR⊥BC,交圆锥底面圆周于R,
则CN=2a=$\sqrt{3}$r,即r=$\frac{2a}{\sqrt{3}}$,
过N作NS∥BC交AQ于S,由△NPS∽△CPR可知QC=NS,又$\frac{NS}{BQ}=\frac{1}{2}$,
∴Q为BC靠近C的三等分点,
∴QR=$\frac{2\sqrt{2}r}{3}$,AQ=$\frac{2\sqrt{7}r}{3}$,AP=$\frac{\sqrt{7}r}{2}$,
∴$\frac{b}{QR}$=$\frac{AP}{AQ}$,∴b=$\frac{\sqrt{2}}{2}$r,即b=$\frac{\sqrt{6}}{3}$a,
∴椭圆面积S=πab=$\frac{{\sqrt{6}π{a^2}}}{3}$.
点评 本题考查了圆锥的结构特征,圆锥的截面曲线,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (0,1)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曹雪芹、莎士比亚、雨果 | B. | 雨果、莎士比亚、曹雪芹 | ||
| C. | 莎士比亚、雨果、曹雪芹 | D. | 曹雪芹、雨果、莎士比亚 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{27}$ | B. | $\frac{2}{27}$ | C. | $\frac{2}{81}$ | D. | $\frac{8}{81}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com