
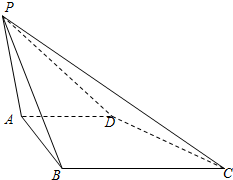
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAD同时垂直侧面PAB与侧面PDC.若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,则$\frac{BC}{AD}$=$\frac{3}{2}$,直线PC与底面ABCD所成角的正切值为$\frac{\sqrt{6}}{6}$.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAD同时垂直侧面PAB与侧面PDC.若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,则$\frac{BC}{AD}$=$\frac{3}{2}$,直线PC与底面ABCD所成角的正切值为$\frac{\sqrt{6}}{6}$. 分析 延长BA,CD交于H,连接PH,运用面面垂直的性质定理,可得PH⊥平面PAD,设PB=$\sqrt{3}$,可得PA=AB=AD=1,运用余弦定理可得∠PAB,在直角三角形HPA中,∠HAP=60°,求得AH,由三角形相似知识,可得$\frac{BC}{AD}$;
求出HP,HD,PD,PC,证得AD⊥PA,又AD⊥AB,AB∩PA=A,即有AD⊥平面PAB,可得BC⊥平面PAB,设P到平面ABCD的距离为d,由VP-ABC=VC-PAB,运用三棱锥的体积公式,求得d,运用同角三角函数的关系,可得直线PC与底面ABCD所成角的正切值.
解答 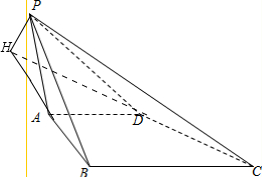 解:延长BA,CD交于H,连接PH,
解:延长BA,CD交于H,连接PH,
可得平面PAB∩平面PCD=PH,
由侧面PAD同时垂直侧面PAB与侧面PDC,
运用面面垂直的性质定理,可得PH⊥平面PAD,
即有HP⊥PA,
设PB=$\sqrt{3}$,
由PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,可得PA=AB=AD=1,
在△PAB中,由余弦定理可得,cos∠PAB=$\frac{1+1-3}{2×1×1}$=-$\frac{1}{2}$,
即有∠PAB=120°,
在直角三角形HPA中,∠HAP=60°,
可得AH=$\frac{AP}{cos∠HAP}$=$\frac{1}{cos60°}$=2,
在三角形HBC中,由三角形的相似知识可得,$\frac{BC}{AD}$=$\frac{HB}{HA}$=$\frac{3}{2}$;
在△HPA中,HP=APtan60°=$\sqrt{3}$,
在直角三角形AHD中,HD=$\sqrt{A{H}^{2}+A{D}^{2}}$=$\sqrt{4+1}$=$\sqrt{5}$,
在直角三角形HPD中,PD=$\sqrt{H{D}^{2}-H{P}^{2}}$=$\sqrt{5-3}$=$\sqrt{2}$,
PA2+AD2=PD2,可得AD⊥PA,
又AD⊥AB,AB∩PA=A,
即有AD⊥平面PAB,
由BC∥AD,可得BC⊥平面PAB,
设P到平面ABCD的距离为d,
由VP-ABC=VC-PAB,可得$\frac{1}{3}$d•S△ABC=$\frac{1}{3}$BC•S△PAB,
即$\frac{1}{3}$d•$\frac{1}{2}$•1•$\frac{3}{2}$=$\frac{1}{3}$•$\frac{3}{2}$•$\frac{1}{2}$•1•1•sin120°,
解得d=$\frac{\sqrt{3}}{2}$,
在直角三角形BCP中,PC=$\sqrt{B{C}^{2}+P{B}^{2}}$=$\sqrt{\frac{9}{4}+3}$=$\frac{\sqrt{21}}{2}$,
可得PC和平面ABCD所成角的正弦值为$\frac{d}{PC}$=$\frac{1}{\sqrt{7}}$,
余弦值为$\sqrt{1-\frac{1}{7}}$=$\frac{\sqrt{6}}{\sqrt{7}}$,
则直线PC与底面ABCD所成角的正切值为$\frac{1}{\sqrt{6}}$=$\frac{\sqrt{6}}{6}$.
故答案为:$\frac{3}{2}$,$\frac{\sqrt{6}}{6}$.
点评 本题考查面面垂直的性质定理的运用,直线和平面所成角的正切值,考查运算能力,运用三角形相似知识和等积法是解题的关键,属于难题.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | 向左平移3个单位 | B. | 向右平移3个单位 | C. | 向左平移1个单位 | D. | 向右平移1个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80m | B. | 20m | C. | 40m | D. | 50m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com