
 如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD.
如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD.分析 (1)连接OD,由半径OD=OA,可得∠OAD=∠ODA;利用平行线的性质OC∥AD,可得∠OAD=∠BOC,进而得到∠DOC=∠ODA.利用三角形全等的判定定理即可得到△DOC≌△BOC.可得∠ODC=∠OBC.利用圆的切线的判定定理即可证明;
(2)从平行线得到线段的比,从而证得.
解答 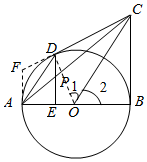 (1)证明:连接OD,
(1)证明:连接OD,
∵OC∥AD,∴∠1=∠ADO,∠2=∠DAO.
∵OA=OD,∴∠ADO=∠DAO,∴∠1=∠2,
∵OC=OC,OB=OD,∴△DOC≌△BOC,∴∠ODC=∠OBC.
∵OB是⊙O的半径,BC是⊙O的切线,
∴BC⊥OB,∴∠OBC=90°,∴∠ODC=90°,
∴CD⊥OD.
又OD是⊙O的半径,∴CD是⊙O的切线.
(2)解:过点A作⊙O的切线AF,交CD的延长线于点F,则FA⊥AB.
∵DE⊥AB,由(1)知CB⊥AB,∴FA∥DE∥CB,∴$\frac{FD}{FC}=\frac{AE}{AB}$.
在△FAC中,∵DP∥FA,∴$\frac{DP}{FA}=\frac{DC}{FC}$.
∵FA,FD是⊙O的切线,∴FA=FD,∴$\frac{DP}{FD}=\frac{DC}{FC}$,∴$\frac{DP}{DC}=\frac{FD}{FC}=\frac{AE}{AB}$.
在△ABC中,∵EP∥BC,∴$\frac{EP}{CB}=\frac{AE}{AB}$.
∵CD,CB是⊙O的切线,∴CB=CD,∴$\frac{EP}{CD}=\frac{AE}{AB}$,∴$\frac{DP}{DC}=\frac{EP}{CD}$,∴DP=EP.
∴点P平分线段DE.
点评 熟练掌握圆的性质、平行线的性质、全等三角形的判定及其性质定理、圆的切线的性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:
设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:| i | 1 | 2 | 3 | 4 | 5 | 合计 |
| xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
| wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
| yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| $\overline{x}$=1.56,$\overline{w}$=4.01,$\overline{y}$=6,$\sum_{i=1}^{5}$xiyi=48.66,$\sum_{i=1}^{5}$wiyi=132.62,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=0.20,$\sum_{i=1}^{5}$(wi-$\overline{w}$)2=10.14 | ||||||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且$\overrightarrow{AF}•\overrightarrow{FB}$=1,|OF|=1.
如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且$\overrightarrow{AF}•\overrightarrow{FB}$=1,|OF|=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3i | B. | 3+2i | C. | -2i | D. | 2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{3}{2}$) | B. | (1,$\frac{3}{2}$] | C. | [1,$\frac{3}{2}$) | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com