
分析 (Ⅰ)求导函数,利用f(x)在x=2处的切线方程为y=9x-14,建立方程,求a,b的值;
(Ⅱ)求出函数的解析式,利用导数的正负可得函数的单调区间;对任意x1∈[0,2],均存在x2∈[0,2]l,使得f(x1)<g(x2)成立,有f(x)max<g(x)max,求出相应函数的最值,即可求得实数k的取值范围.
解答 解:(Ⅰ)求导函数可得f′(x)=3x2-3a,
∵f(x)在x=2处的切线方程为y=9x-14,
∴$\left\{\begin{array}{l}{f(2)=8-6a+b=4}\\{f′(2)=12-3a=9}\end{array}\right.$,∴a=1,b=2,
(Ⅱ)由(Ⅰ)知,f(x)=x3-3x+2
∴f′(x)=3(x+1)(x-1),
由f′(x)>0,得x<-1或x>1;由f′(x)<0,得-1<x<1.
故函数f(x)单调递减区间是(-1,1);单调递增区间是(-∞,-1),(1,+∞).
∴函数f(x)在(0,1)单调递减,在(1,2)上单调递增,
又f(0)=2,f(2)=4,有f(0)<f(2),
∴函数f(x)在区间[0,2]上的最大值f(x)max=f(2)=4.
又g(x)=-ex+k2+4k
∴g′(x)=-ex,
∴函数g(x)在[0,2]上单调递减,最大值为g(x)max=g(0)=k2+4k-1
因为对任意x1∈[0,2],均存在x2∈[0,2]l,使得f(x1)<g(x2)成立,
所以有f(x)max<g(x)max,则4<k2+4k-1,
∴k>1或k<-5.
故实数k的取值范围是(-∞,-5)∪(1,+∞).
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查函数的最值,解题的关键是将问题转化为f(x)max<g(x)max,属于中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD.
如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
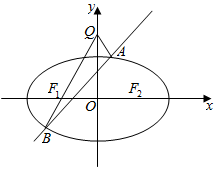 如图,点F1,F2分别为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,椭圆E上任意一点到左焦点的距离的取值范围为[2-$\sqrt{2}$,2+$\sqrt{2}$],直线l:y=kx+1与椭圆相交于A,B两点.
如图,点F1,F2分别为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,椭圆E上任意一点到左焦点的距离的取值范围为[2-$\sqrt{2}$,2+$\sqrt{2}$],直线l:y=kx+1与椭圆相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $\frac{7}{8}$或$-\frac{7}{8}$ | D. | $\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{3}{4},2]$ | B. | $(-∞,\frac{3}{4}]∪[2,+∞)$ | C. | (-∞,1]∪[2,+∞) | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
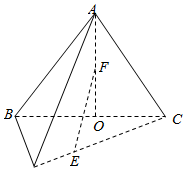 如图,在三棱锥A-BCD中,O是BC中点,AO⊥平面BCD,CD⊥BD,∠BCD=$\frac{π}{6}$,BC=2,OA=$\sqrt{2}$,CE=3ED,F是OA的中点.
如图,在三棱锥A-BCD中,O是BC中点,AO⊥平面BCD,CD⊥BD,∠BCD=$\frac{π}{6}$,BC=2,OA=$\sqrt{2}$,CE=3ED,F是OA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com