
 如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且$\overrightarrow{AF}•\overrightarrow{FB}$=1,|OF|=1.
如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且$\overrightarrow{AF}•\overrightarrow{FB}$=1,|OF|=1.分析 (1)设椭圆的标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,则c=1.由$\overrightarrow{AF}•\overrightarrow{FB}=1$,即(a+c)•(a-c)=1=a2-c2,可得a2,b2=a2-c2,即可得出.
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,设P(x1,y1),Q(x2,y2),kPQ=1.可设直线l的方程为y=x+m.与椭圆方程联立得3x2+4mx+2m2-2=0.又F为△PQM的垂心,可得MP⊥FQ.∴$\overrightarrow{MP}•\overrightarrow{FQ}$=0,利用根与系数的关系即可得出.
解答 解:(1)设椭圆的标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,则c=1.
又∵$\overrightarrow{AF}•\overrightarrow{FB}=1$,即(a+c)•(a-c)=1=a2-c2,
∴a2=2,b2=1.
故椭圆的标准方程为$\frac{x^2}{2}+{y^2}=1$.
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,
设P(x1,y1),Q(x2,y2),
∵M(0,1),F(1,0),∴kPQ=1.
∴设直线l的方程为y=x+m.
由$\left\{{\begin{array}{l}{y=x+m}\\{{x^2}+2{y^2}=2}\end{array}}\right.$,得3x2+4mx+2m2-2=0.
又F为△PQM的垂心,∴MP⊥FQ.
∴$\overrightarrow{MP}•\overrightarrow{FQ}={x_1}({x_2}-1)+{y_2}({y_1}-1)=0$.
又yi=xi+m(i=1,2),
∴x1(x2-1)+(x2+m)(x1+m-1)=0,
即$2{x_1}{x_2}+({x_1}+{x_2})(m-1)+{m^2}-m=0$.
由根与系数的关系,得$2•\frac{{2{m^2}-2}}{3}-\frac{4m}{3}(m-1)+{m^2}-m=0$.
解得$m=-\frac{4}{3}$或m=1(舍去),经检验$m=-\frac{4}{3}$符合条件.
故存在直线l,使点F恰为△PQM的垂心,且直线l的方程为$y=x-\frac{4}{3}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为一元二次方程的根与系数的关系、向量垂直与数量积的关系、三角形垂心的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
| 高血压 | 非高血压 | 总计 | |
| 年龄20到39岁 | 12 | c | 100 |
| 年龄40到60岁 | b | 52 | 100 |
| 总计 | 60 | a | 200 |
| P(k2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
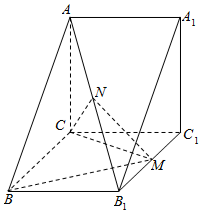 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,M是棱B1C1的中点,N是对角线AB1的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,M是棱B1C1的中点,N是对角线AB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD.
如图,AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $\frac{7}{8}$或$-\frac{7}{8}$ | D. | $\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com