
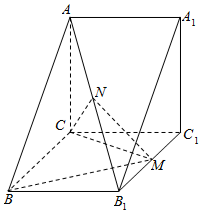
 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,M是棱B1C1的中点,N是对角线AB1的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,M是棱B1C1的中点,N是对角线AB1的中点.分析 (1)推导出AC⊥BC,AC⊥CC1,从而AC⊥平面BCC1B1,连接CA1,NA1,则B、A1、N三点共线,推导出CN⊥BA1,CN⊥MN,由线面垂直的判定定理得CN⊥平面BNM.
(2)连接AC1交CA1于点H,推导出AH⊥BA1,HQ⊥BA1,则∠AQH是二面角A-BA1-C的平面角.由此能求出二面角C-BN-B1的余弦值.
解答  证明:(1)因为AC=1,$BC=\sqrt{2},AB=\sqrt{3}$,
证明:(1)因为AC=1,$BC=\sqrt{2},AB=\sqrt{3}$,
所以AC2+BC2=AB2,即AC⊥BC
又AC⊥CC1,BC∩CC1=C,所以AC⊥平面BCC1B1,
连接CA1,NA1,则B、A1、N三点共线,则$C{A_1}=\sqrt{2}=CB$,
所以△CA1B是等腰三角形,又N是BA1的中点,所以CN⊥BA1.
连接A1M,则RT△BB1M≌RT△A1C1M,A1M=BM,
所以△BA1M是等腰三角形,
所以MN⊥A1B.因为$BM=\sqrt{1+{{(\frac{{\sqrt{2}}}{2})}^2}}=\frac{{\sqrt{6}}}{2},BN=\frac{1}{2}{A_1}B=1$,
由勾股定理得$MN=\frac{{\sqrt{2}}}{2}$,即${C_1}M=MN=\frac{{\sqrt{2}}}{2}$.
在△MCN和△CC1M中,$CN=\frac{1}{2}{A_1}B=1={C_1}C,{C_1}M=MN,CM=CM$,
所以△MCN≌△MCC1,因为∠CC1M=90°,所以∠CNM=90°,即CN⊥MN
又BN∩NM=N,所以依据线面垂直的判定定理得CN⊥平面BNM.
解:(2)依题意CB⊥平面ACC1A1,连接AC1交CA1于点H,因为侧面ACC1A1是正方形,
所以AC1⊥CA1,所以AH⊥平面BCA1,即AH⊥BA1.
取线段NA1的中点Q,连接HQ、AQ,则HQ是△CA1N的中位线,HQ∥CN,
由(1)知CN⊥A1B,所以HQ⊥BA1,所以BA1⊥平面AHQ,
则∠AQH是二面角A-BA1-C的平面角.
因为CN=1,所以$HQ=\frac{1}{2}$,
在△BA1A中,${A_1}A=1,AB=\sqrt{3},{A_1}B=2,{A_1}{A^2}+A{B^2}={A_1}{B^2}$,
所以△BA1A为直角三角形,则$AQ=\frac{{\sqrt{3}}}{2}$,
所以$cos∠AQH=\frac{QH}{AQ}=\frac{{\sqrt{3}}}{3}$,
又二面角C-BN-B1的平面角是∠AQH的补角,
所以二面角C-BN-B1的余弦值是$-\frac{{\sqrt{3}}}{3}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且$\overrightarrow{AF}•\overrightarrow{FB}$=1,|OF|=1.
如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且$\overrightarrow{AF}•\overrightarrow{FB}$=1,|OF|=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{3}{2}$) | B. | (1,$\frac{3}{2}$] | C. | [1,$\frac{3}{2}$) | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
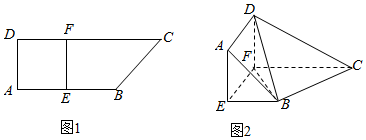 如图1,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AE=1,AB=2,CD=3,E,F分别为AB,CD上的点,以EF为轴将正方形ADFE向上翻折,使平面ADFE与平面BEFC垂直如图2.
如图1,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AE=1,AB=2,CD=3,E,F分别为AB,CD上的点,以EF为轴将正方形ADFE向上翻折,使平面ADFE与平面BEFC垂直如图2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com