
分析 (1)求出函数的导数,解关于a,b的方程组,求出a,b的值,从而求出函数的解析式即可;
(2)求出函数的导数,得到函数的单调区间,计算函数值,求出n的值即可;
(3)将a=1代入f(x),通过作差法和换元法结合函数的单调性证明即可.
解答 解:(1)$f'(x)=2x+b-\frac{a}{x}$,所以$\left\{{\begin{array}{l}{f'(1)=2+b-a=-5}\\{f(1)=1+b=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{b=-1}\\{a=6}\end{array}}\right.$,
∴函数f(x)的解析式为f(x)=x2-x-6lnx(x>0);…(3分)
(2)$f(x)={x^2}-x-6lnx⇒f'(x)=2x-1-\frac{6}{x}=\frac{{2{x^2}-x-6}}{x}$,
因为函数f(x)的定义域为x>0,
令$f'(x)=\frac{{({2x+3})({x-2})}}{x}=0⇒x=-\frac{3}{2}或x=2$,
当x∈(0,2)时,f'(x)<0,f(x)单调递减,
当x∈(2,+∞)时,f'(x)>0,函数f(x)单调递增,
且函数f(x)至少有1个零点,而f(1)=0,不符合要求,
$f(3)=6({1-ln3})<0,f(4)=6({2-ln4})=6ln\frac{e^2}{4}>0$,
∴x0∈(3,4),故n=3…(7分)
(3)当a=1时,函数f(x)=x2+bx-lnx,
$f({x_1})=x_1^2+b{x_1}-ln{x_1}=0,f({x_2})=x_2^2+b{x_2}-ln{x_2}=0$,
两式相减可得:$x_1^2-x_2^2+b({{x_1}-{x_2}})-ln{x_1}+ln{x_2}=0,b=\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}-({{x_1}+{x_2}})$…(9分)
$f'(x)=2x+b-\frac{1}{x},f'({x_0})=2{x_0}+b-\frac{1}{x_0}$,
因为${x_0}=\frac{{{x_1}+{x_2}}}{2}$,
所以$f'({x_0})=2×\frac{{{x_1}+{x_2}}}{2}+\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}-({{x_1}+{x_2}})-\frac{2}{{{x_1}+{x_2}}}$,
$\begin{array}{l}=\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}-\frac{2}{{{x_1}+{x_2}}}=\frac{1}{{{x_2}-{x_1}}}[{ln{x_2}-ln{x_1}-\frac{{2({{x_2}-{x_1}})}}{{{x_1}+{x_2}}}}]\\=\frac{1}{{{x_2}-{x_1}}}[{ln\frac{x_2}{x_1}-\frac{{2({\frac{x_2}{x_1}-1})}}{{\frac{x_2}{x_1}+1}}}]\end{array}$
设$\frac{x_2}{x_1}=t>1,h(t)=lnt-\frac{{2({t-1})}}{t+1}$,
∴$h'(t)=\frac{1}{t}-\frac{4}{{{{({t+1})}^2}}}=\frac{{{{({t+1})}^2}-4t}}{{t{{({t+1})}^2}}}=\frac{{{{({t-1})}^2}}}{{t{{({t+1})}^2}}}>0$,
所以h(t)在(1,+∞)上为增函数,且h(1)=0,
∴h(t)>0,又$\frac{1}{{{x_2}-{x_1}}}>0$,所以f'(x0)>0…(12分)
点评 本题考查了曲线的切线方程问题,函数的单调性、最值问题,考查导数的应用以及换元思想的应用,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{1024}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}i$ | B. | -$\frac{3}{5}$i | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
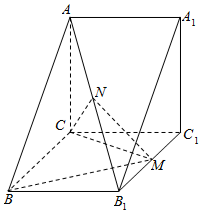 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,M是棱B1C1的中点,N是对角线AB1的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,M是棱B1C1的中点,N是对角线AB1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com